Molecular Orbital Theory

MOLECULAR ORBITAL THEORY (MOT) or M.O. Theory.

The molecular orbital theory was developed by Hund and Mulliken, later developed by Lennard Jones and Coulson. There is a saying that when they tried to explain the paramagnetic nature of oxygen molecule this theory originated. It is The basic question that arises in every one is when molecule is formed what changes takes place in the electrons and nuclei of the atoms participated. It is because the molecule has different properties compared to those of participant atoms. That means it must have its own electronic arrangement and position of nuclei. If only participating electrons are involved why should all properties change?.

According to the molecular orbital theory, which is modern and more rational, a molecule is considered to be quite different from the constituent atoms. All the electrons belonging to the atoms constituting a molecule are considered to be moving along the entire molecule under the influence of all the nuclei. Thus, a molecule is supposed to have orbitals of varying energy levels in the same way as an isolated atom has. These orbitals are called molecular orbitals. Molecular orbital is polycentric.

The molecular orbitals are filled in the same way as the atomic orbitals, following the ‘aufbau’ and Pauli exclusion principles. Thus, a molecular orbital, like an atomic orbital, can contain a maximum number of two electrons and the two electrons have opposite spins.

The difference between an atomic orbital and a molecular orbital is that while an electron in an atomic orbital is influenced by one positive nucleus, an electron in a molecular orbital is influenced by two or more nuclei depending upon the number of atoms contained in a molecule. According to wave mechanics, the atomic orbitals can be expressed by wave functions (Ψ ),which represent the amplitude of waves.

According to M.O. theory, the molecular orbitals are formed by the linear combination of atomic orbitals(L.C.A.O) of the atoms which form the molecule. Those orbitals must have nearly equal or energies and proper symmetry.

For example, consider a hydrogen molecule consisting of two atoms labeled as H_A and H_B. Let the wave functions for the electrons in the atomic orbitals of two atoms A and B is Ψ_A and Ψ_B, respectively. When these atomic orbitals are brought closer, they combine to form molecular orbitals. The wave function Ψ for electron in the field of nuclei of atoms A and B (i.e, corresponding to the molecular orbital) may be written as a suitable linear combination of wave functions Ψ_A and Ψ_B. As discussed earlier, may be expressed in two ways.

Ψ = Ψ_A + Ψ_B and Ψ^* = Ψ_A – Ψ_B

Where Ψ corresponds to wave function for symmetric combination whereas Ψ^* corresponds to wave function for antisymmetric combination.

Now Ψ² and (Ψ^*)² give probabilities of finding electrons in the two molecular orbitals formed according to the equations shown below respectively.

Ψ² = (Ψ_A + Ψ_B)² = Ψ_A² + Ψ_B² + 2 Ψ_A Ψ_B

(Ψ^*)² = Ψ_A² + Ψ_B² – 2 Ψ_A Ψ_B

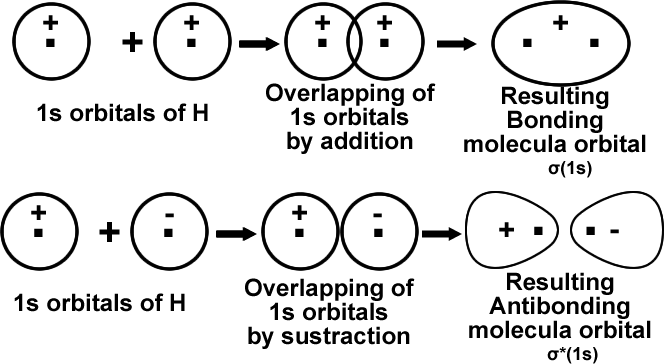
It is evident that Ψ² is greater that Ψ_A² + Ψ_B² by an amount equal to2 Ψ_A Ψ_B. That means the probability of locating electron is greater than either of the atomic orbitals Ψ_A and Ψ_B. That is it has lower energy than either of the atomic orbitals. This leads to stable bond formation. B.M.O (σ).

During the formation of BMO, the two electron waves of the bonding atoms reinforce each other due to constructive interference. High electron density between the nuclei which minimize repulsion and holds them together.

During the formation of ABMO, the electron waves cancel each other due to destructive interference. Least electron density between the nuclei.

That means the molecular orbital formed by symmetric combination of orbitals is more stable and is termed as bonding molecular orbital (σ). The other is antisymmetric combination of orbitals and is termed as antibonding molecular orbital (σ^*).

The physical picture of these two types of MOS can be shown with, a simple case of combination of ls orbital of one hydrogen atom with 1s orbital of another hydrogen atom.

Molecular orbitals from ‘2s’ Atomic orbitals: just like the combination of ‘1s’ atomic orbitals, ‘2s’ atomic orbitals also combine in two ways to form ‘σ(2s)’bonding M.O and ‘σ^*(2s)’ A.B.M.O.

Combination of p-atomic orbitals: There are three p-atomic orbitals represented as p_x, p_y and p_z .

As a convention, the Z- axis is taken as the internuclear axis.

The X and Y axes would then be perpendicular to the nuclear axis. The combination of p_z orbitals would lead to the formation of σ(2p_z) bonding MO and antibonding MO σ^*(2p_z) as shown below.

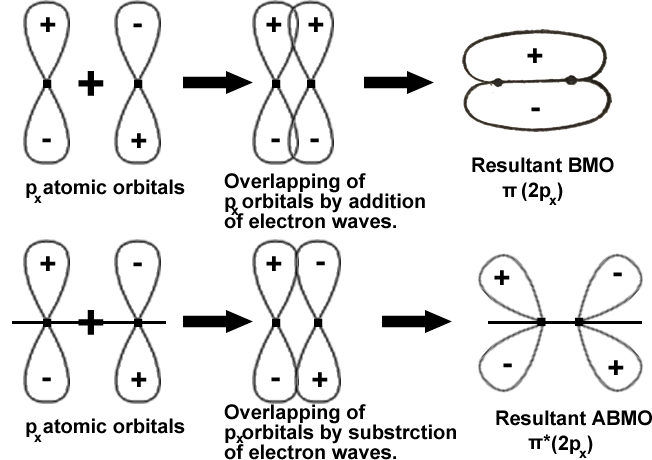
The formation of π(2p_y) = the formation of π(2p_x) and

The formation of π^*(2p_y) = the formation of π^*(2p_x).

The difference between BMO and ABMO:

BMO	ABMO
Formed by the addition overlap of atomic orbitals.	Formed by the sustraction overlap of atomic orbitals.
Energy lower than the parent AOs.	Energy more than the parent AOs.
Electron density in between the nuclei is high. It is located between the nuclei of the bonded atoms which accounts for the stability of the bond.	Electron density in between the nuclei is very less. It is located away from the space between nuclei (nodal plane) and hence the repulsion between the nuclei is high. Which accounts for the least stability of the bond.

Differences between σ and π MO’s:

σ Molecular orbital	π Molecular orbital
1. Formed by the end on overlap along the internuclear axis.	1. Formed by the side wise o v e r l a p perpendicular to inter nuclear axis.
2. Overlapped region is very large.	2. Overlapped region is small.
3. Rotation about the internuclear axis is symmetrical.	3. Rotation about the inter nuclear axis is unsymmetrical.
4. Strong bonds are favoured.	4. Weak bonds are favoured.

1. A bonding MO is formed by the addition-overlap of atomic orbitals. The electron density in between the nuclei is high which accounts for the stability of the bond formed. It has lower energy than the AOS from which it is formed.

2.An antibonding MO is formed by the subtraction-overlap of atomic orbitals. It has higher energy than the AOS from which it is formed.The electron density in between the nuclei is very low and hence the repulsion between the nuclei is high. The formation of a bond, therefore, is not possible.

Conditions for the Combination of Atomic Orbitals:

It should be noted that any two atomic orbitals will not essentially combine to form molecular orbitals. There are, in fact, certain limitations to the combination of atomic orbitals which are summed up below.

1. The energy of the AOs involved should not differ much from one another. Thus in the formation of a homonuclear diatomic molecule of the type A₂, 1s-orbital of one atom does not combine with 2s-orbital of another atom of the same element. Likewise, 2s-orbital of one atom does not combine with 2p-orbital of another atom of the same element. In the case of heteronuclear diatomic molecules of the type AB, however, such combinations may be possible.

2. The AOs combine only if they overlap to a considerable extent. This overlap brings high electron cloud in between the two nuclei thereby minimising their mutual repulsion.

3. The AOs should have the same symmetry about the molecular axis a P_x (or P_y) orbital of one atom does not combine with an s-orbital of another atom. This is illustrated in Fig.

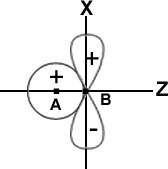
The s-orbital of an atom A is shown to overlap with the P_x -orbital of another atom B. But, since the molecular axis is in the Z direction and the p_x orbital is oriented at right angles to this axis, no combination is possible. Thus, no molecular Z orbital can result in spite of the overlap. In fact, the ++ overlap is cancelled by the+-overlap, as shown in the figure.

Similarly, a P_y orbital does not combine with an s-orbital as they have different symmetry.

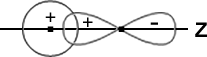
A ‘P_z’ orbital, however, is able to combine with an s orbital since they have the same symmetry, as shown in Fig.

The following chart gives a clear idea how‘s’ & ‘p’ can combine with each other to form molecular orbitals (assuming Z-axis as inter nuclear axis).

First orbital	Second orbital	Type of MO formed
s	s, pz	σ
pz	s, pz	σ
px	px	π
py	py	π

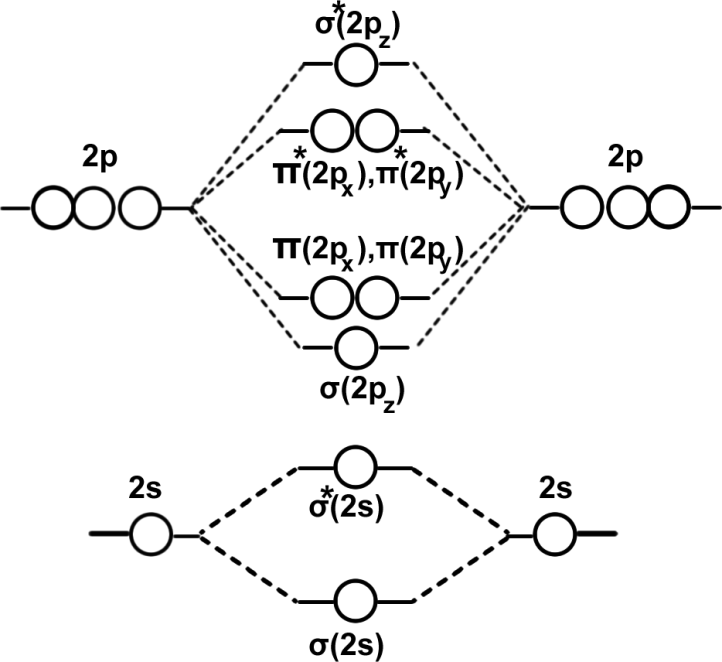
Energy level diagram of Molecular Orbitals:

We have learnt that ‘1s’ atomic orbitals of two atoms form two MOs designated as σ(1s)and σ^*(1s). The ‘2s’ and ‘2p’ orbitals form eight MOs.

BMO	σ(2s)	σ(2pz)	π(2px)	π(2py)
ABMO	σ*(2s)	σ*(2pz)	π*(2px)	π*(2py)

The energy levels of the orbitals have been determined experimentally from spectroscopic data. The energy levels of different molecular orbitals are shown diagrammatically in the following figure. In this diagram, the molecular orbitals are shown in the centre and the atomic orbitals which combine are shown on the two extremes. The atomic orbitals of same energy are shown at the same level while the bonding MOs are shown lower and the antibonding MOs are shown higher than the corresponding atomic orbitals. This indicates that while the bonding MOS are more stable, the antibonding MOS are less stable than the AOS from which they are formed. It is clear from the figure that the extent of stabilization for a bonding MO is always equal to the extent of destabilization for the corresponding antibonding MO.

The following is the order of energies of MOs is correct for molecules having electrons less than or equal to 14 electrons. Eg: Li­₂,Be₂,B₂,C₂,N₂.

For molecules having less than 14 electrons the order of energies of MOs is as shown below. Eg: O₂,F₂.

You may get a doubt why this difference though they ‘2s’ and’2p’ orbitals.

Energy differences of ‘2s’ and ‘2p’ AOs of second row elements
Atoms	Li	Be	B	C	N	O	F
Energy difference	178	262	449	510	570	1430	1970

It is clear from the above table that energy difference is less up to ‘N’ and from then it becomes significantly large.

Rules for filling of electrons in MOs:

In MO theory we consider the whole molecule rather than the constituent atoms and use MOs than AOs.

1. The MO with lowest energy is filled first.

2.Maximum number of electrons in any MO is ‘2’ with opposite spins.

3. If two or more MOs have same energy pairing takes place only all of them get one electron.

Bond order:

It accounts for the stability of the molecule and can be calculated as follows.

Bond order =

[Number of electrons in BMOs(N_b) – Number of electrons in ABMOs(N_a)].

A positive bond order is N_b>N_a means a stable molecule. 1, 2 & 3 values indicate single double and triple bonds.

While a negative (N_b<N_a) or zero (N_b=N_a) bond order means an unstable molecule and bond is not formed.

If Bond order↑ , Bond energy ↑,stability of a molecule ↑,bond length ↓.

Now let us consider the MO picture of molecules individually.

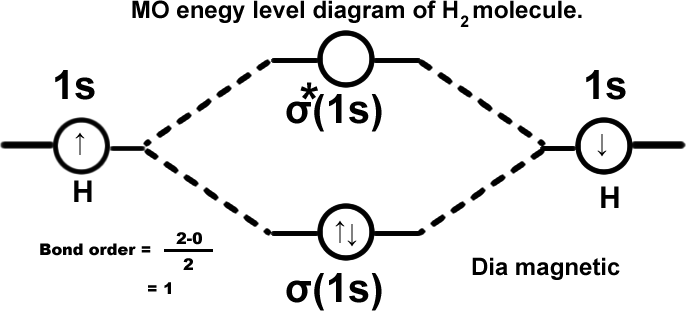
Hydrogen molecule.(H₂) σ(1s²).

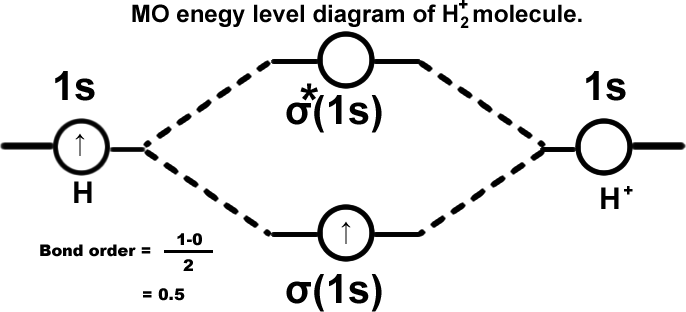
Hydrogen molecule ion.(H₂⁺) σ(1s¹). This can exist but less stable than H₂. However it is detected spectroscopically when hydrogen gas under pressure is subjected to electric discharge.

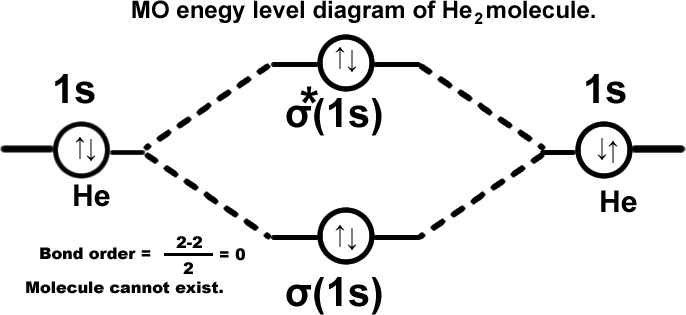
Helium molecule. (He₂) σ(1s²),σ^*(1s²). Molecule cannot exist.

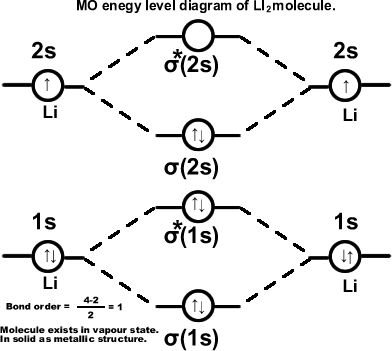
Lithium molecule. (Li₂) σ(1s²),σ^*(1s²),σ(2s²). Molecule exists in vapour state.

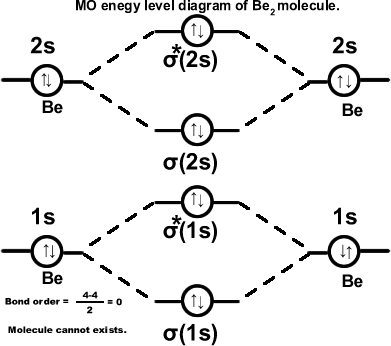
Beryllium molecule. (Be₂) σ(1s²),σ^*(1s²),σ(2s²),σ^*(2s²). Molecule cannot exist.

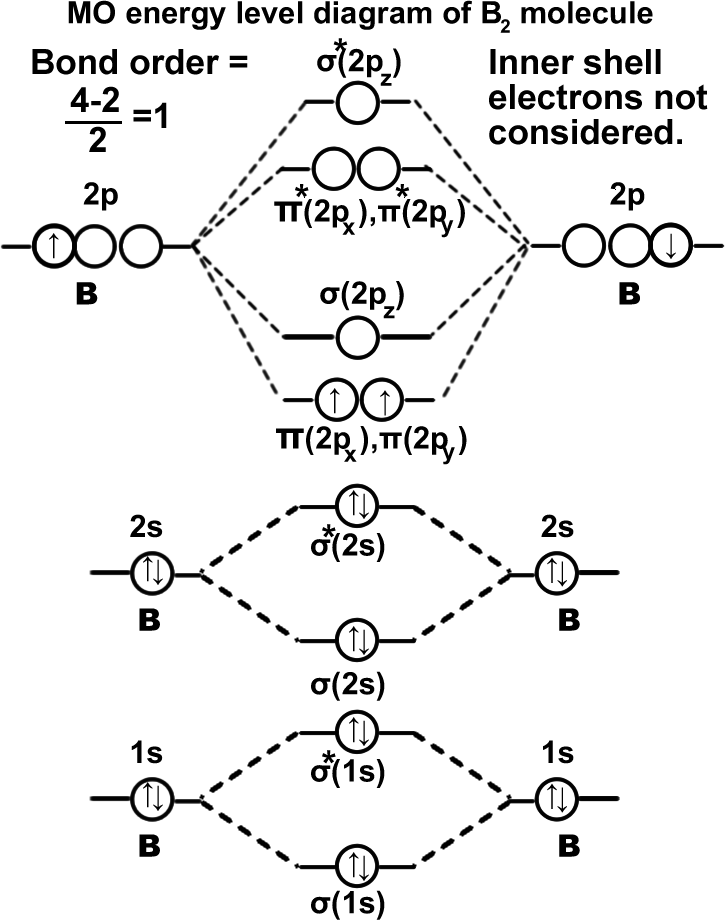
Boran molecule. (B₂). σ(1s²),σ^*(1s²),σ(2s²),σ^*(2s²),π(2p_x¹)=π(2p_y¹). Molecule can exist.

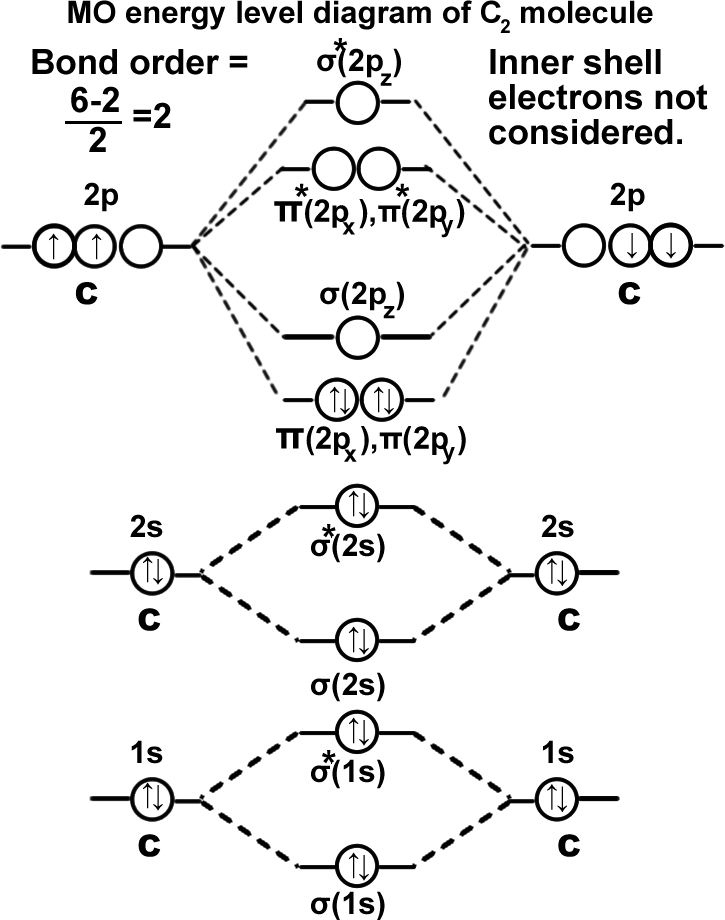
Carbon molecule. (C₂): σ(1s²),σ^*(1s²),σ(2s²),σ^*(2s²),π(2p_x¹)=π(2p_y¹). It can be written as KK σ(2s²),σ^*(2s²),π(2p_x¹)=π(2p_y¹). Molecule should be stable since the bond order is ‘2’. In fact carbon exists as a macromolecule in graphite and diamond which contains much more stable structure since carbon is making ‘3’ σ bonds in graphite and ‘4’ σ bonds in diamond.

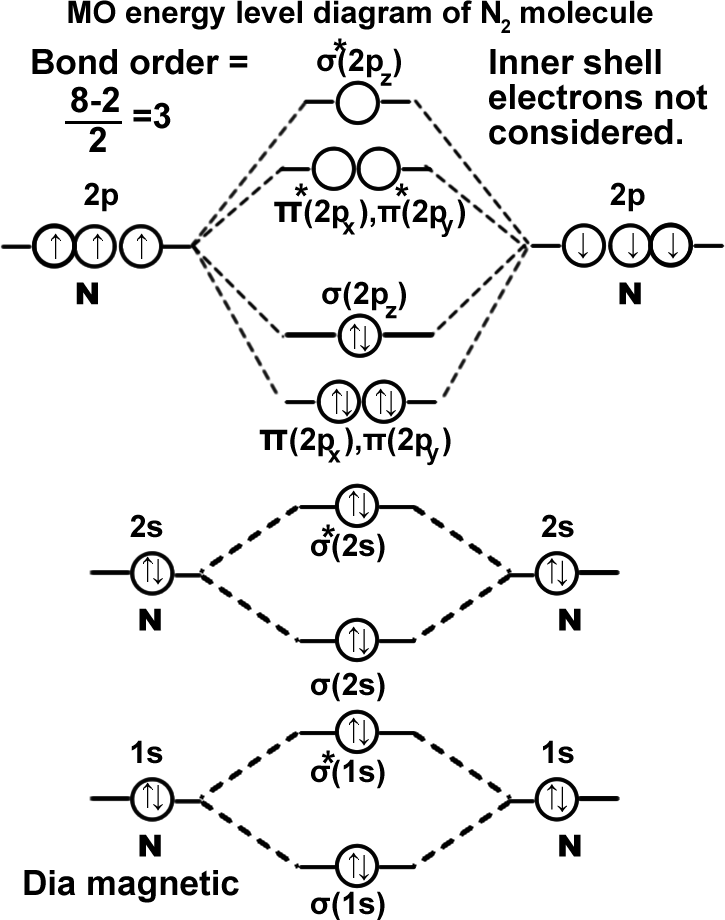
Nitrogen molecule. (N₂). σ(1s²),σ^*(1s²),σ(2s²),σ^*(2s²), π(2p_x²)=π(2p_y²), σ(2p_z²). It can be written as KK σ(2s²),σ^*(2s²), π(2p_x²)=π(2p_y²), σ(2p_z²). Molecule exists as NN.

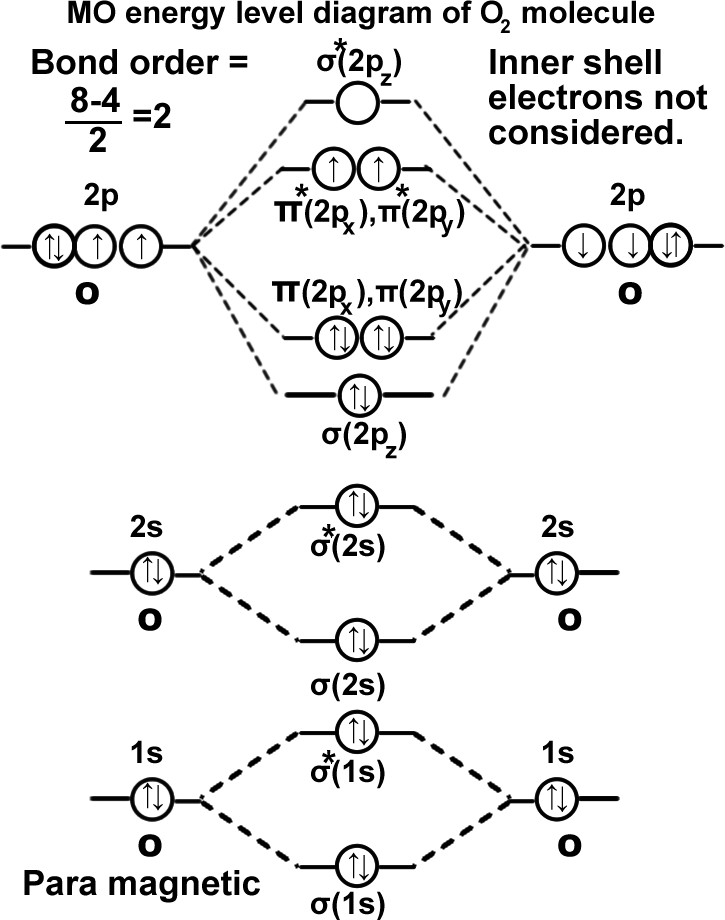
Oxygen molecule. (O₂).

σ(1s²),σ^*(1s²),σ(2s²),σ^*(2s²),σ(2p_z²), π(2p_x²)=π(2p_y²),π^*(2p_x¹)=π^*(2p_y¹). It can be written as KK σ(2s²),σ^*(2s²),σ(2p_z²), π(2p_x²)=π(2p_y²),π^*(2p_x¹)=π^*(2p_y¹). Molecule exists as O=O. as there are two unpaired electrons in π^*ABMOs the molecule is para magnetic. The magnetic character cannot be explained by valance bond theory which says all electrons are paired.

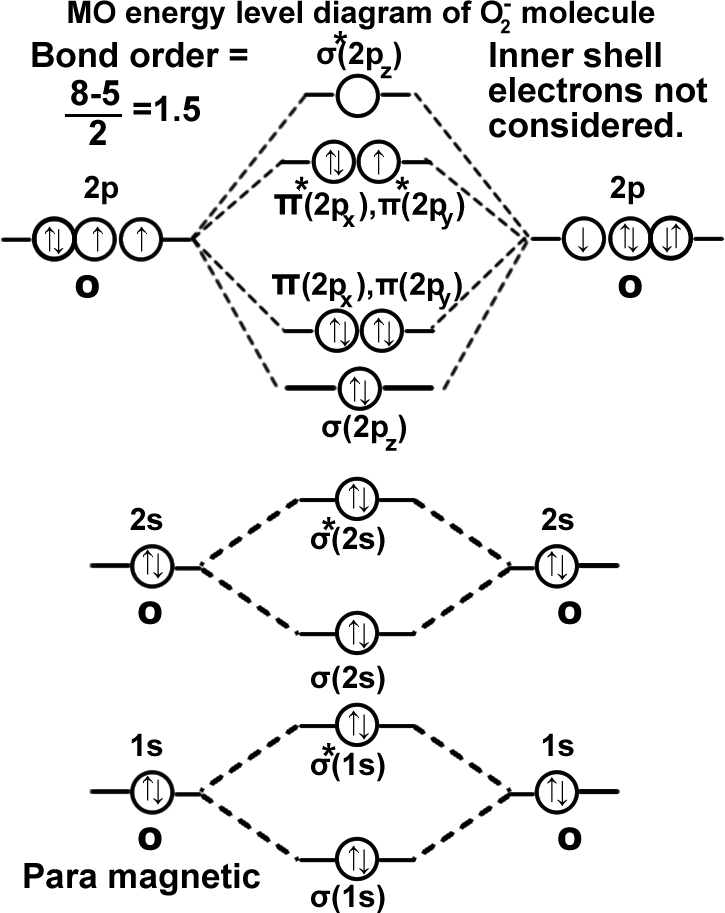
(O₂)^– ion. Superoxide ion.

The compound potassium superoxide KO₂, contains the superoxide ion O₂^– ion. It has 17 electrons, and has one more electron than the O₂ molecule. This extra electron occupies either the π^*(2p_x) , or π*(2р_y), orbital. It does not matter which it occupies since they are the same energy.

σ(1s²),σ^*(1s²),σ(2s²),σ^*(2s²),σ(2p_z²), π(2p_x²)=π(2p_y²),π^*(2p_x²)=π^*(2p_y¹). It can be written as KK σ(2s²),σ^*(2s²),σ(2p_z²), π(2p_x²)=π(2p_y²),π^*(2p_x²)=π^*(2p_y¹).

The bond order = 1½, this corresponds to a bond that is intermediate in length between a single and a double bond. Alternatively the bond order may be calculated as (bonding – antibonding)/2, that is (10-7)/2= 1.5

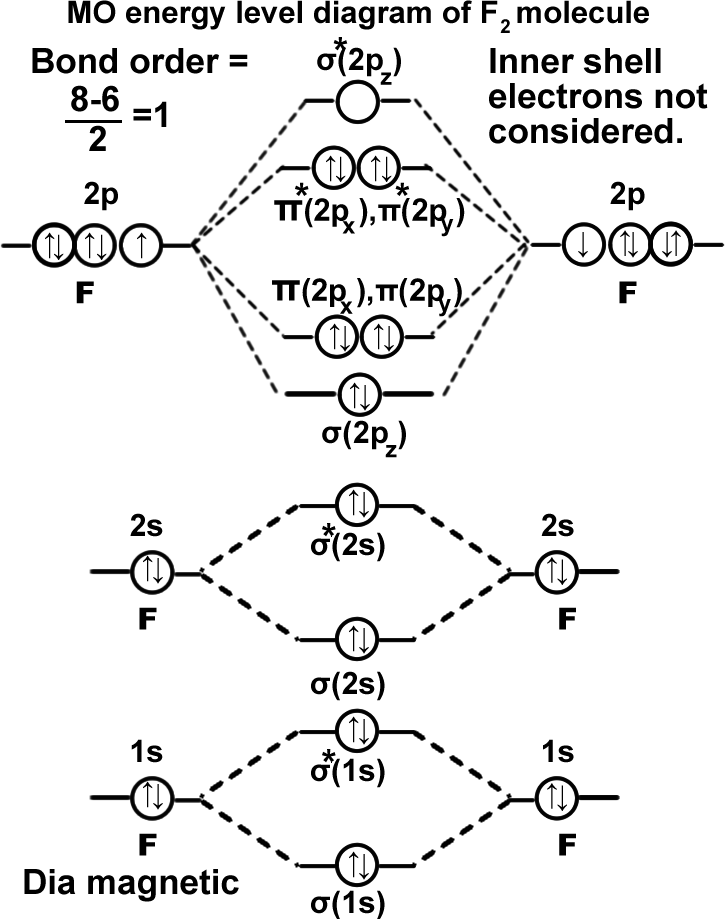
Fluorine molecule. (F₂).

σ(1s²),σ^*(1s²),σ(2s²),σ^*(2s²),σ(2p_z²), π(2p_x²)=π(2p_y²),π^*(2p_x²)=π^*(2p_y²). It can be written as KK σ(2s²),σ^*(2s²),σ(2p_z²), π(2p_x²)=π(2p_y²),π^*(2p_x²)=π^*(2p_y²). Molecule exists as F-F

Now with help of the above knowledge of writing electronic arrangement in BMOs and ABMOs let us try the following.

N₂^2- ion: 19 electrons.

KK σ(2s²),σ^*(2s²), π(2p_x²)=π(2p_y²), σ(2p_z²).π^*(2p_x¹ ) = π^*(2p_y¹ ).

Bond order =(8-4) = 2.

N₂^1- ion: 18 electrons.

KK σ(2s²),σ^*(2s²), π(2p_x²)=π(2p_y²), σ(2p_z²).π^*(2p_x¹ ) = π^*(2p_y⁰ ).

Bond order =(8-3) = 2.5.

N₂¹⁺ ion: 13 electrons.

KK σ(2s²),σ^*(2s²), π(2p_x²)=π(2p_y²), σ(2p_z¹).π^*(2p_x⁰ ) = π^*(2p_y⁰ ).

Bond order =(7-2) = 2.5.

N₂²⁺ ion: 12 electrons.

KK σ(2s²),σ^*(2s²), π(2p_x²)=π(2p_y²), σ(2p_z⁰).π^*(2p_x⁰ ) = π^*(2p_y⁰ ).

Bond order =(6-2) = 2.

As the bond order increases the stability of molecule increase. However, some of the bond orders are identical. In such case, a molecule or ion with more number of electrons in their antibonding orbitals is less stable.

N₂^2- < N₂²⁺ < N₂^1- < N₂¹⁺ < N₂.

Bond dissociation energy order: N₂ > N₂¹⁺ = N₂^1- > N₂^2-.

Bond length order: N₂^2- > N₂^1- = N₂¹⁺ > N₂.

Oxygen molecule(O₂):

KK σ(2s²),σ^*(2s²),σ(2p_z²), π(2p_x²)=π(2p_y²),π^*(2p_x¹)=π^*(2p_y¹).

Bond order = (8-4) = 2

O₂⁺¹ ion: KK σ(2s²),σ^*(2s²),σ(2p_z²), π(2p_x²)=π(2p_y²),π^*(2p_x¹)=π^*(2p_y⁰).

Bond order = (8-3) = 2.5.

O₂^-1 ion: KK σ(2s²),σ^*(2s²),σ(2p_z²), π(2p_x²)=π(2p_y²),π^*(2p_x²)=π^*(2p_y¹).

Bond order = (8-5) = 1.5.

O₂^-2 ion: KK σ(2s²),σ^*(2s²),σ(2p_z²), π(2p_x²)=π(2p_y²),π^*(2p_x²)=π^*(2p_y²).

Bond order = (8-6) = 1.0.

Among these four O₂⁺¹ ion has more bond order and less bond length.

Bond dissociation energy order: O₂⁺¹ > O₂ > O₂^-1 > O₂^-2.

Bond length order: O­₂^-2 > O₂^-1 >O₂ > O₂⁺¹.

EXAMPLES OF MOLECULAR ORBITAL TREATMENT FOR HETERONUCLEAR DIATOMIC MOLECULES OVE

The same principles apply when combining atomic orbitals from two different atoms as applied when the atoms were identical, that is:

1. Only atomic orbitals of about the same energy can combine effectively

2. They should have the maximum overlap.

3. They must have the same symmetry.

Since the two atoms are different, the energies of their atomic orbitals are slightly different. A diagram showing how they combine to form molecular orbitals after considering the symmetry interaction of 2s and 2p, orbitals is given in below taking ‘CO’ and ‘NO’ molecules as example. In these diagrams the energies of AOs of the element with more electro negativity is shown lower level and the A Os of the element with less electro negativity is shown at higher level.

The problem is that in many cases the order of MO energy levels is not known with certainty. Thus we will consider first some examples where the two different atoms are close to each other in the periodic table, and consequently it is reasonable to assume that the order of energies for the MOS are the same as for homonuclear molecules.

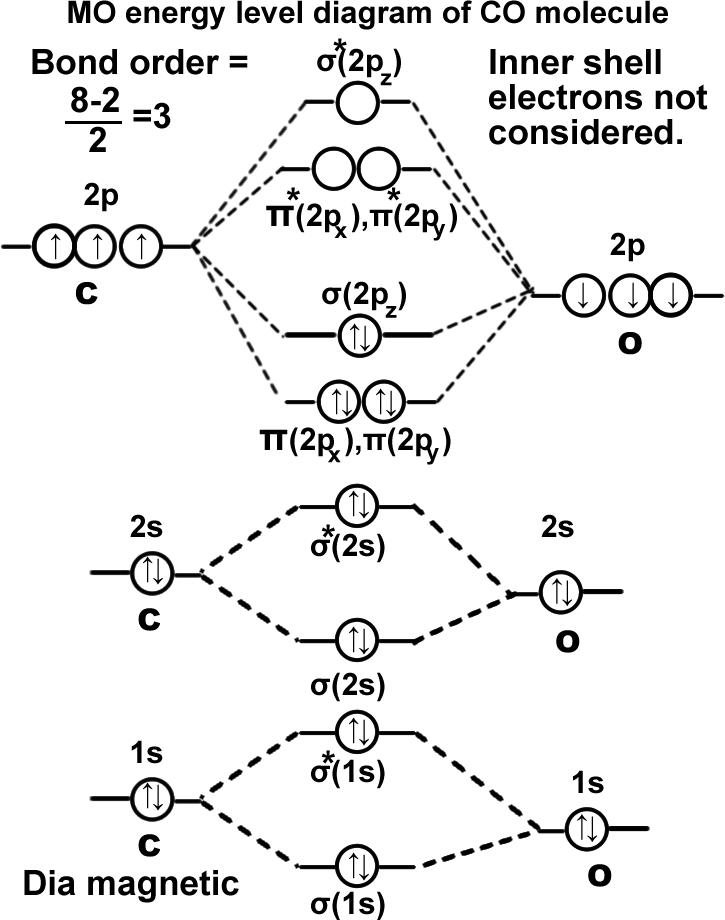
Carbon monoxide molecule. (CO).

σ(1s²),σ^*(1s²),σ(2s²),σ^*(2s²), π(2p_x²)=π(2p_y²), σ(2p_z²). It can be written as KK σ(2s²),σ^*(2s²), π(2p_x²)=π(2p_y²), σ(2p_z²). Molecule exists.

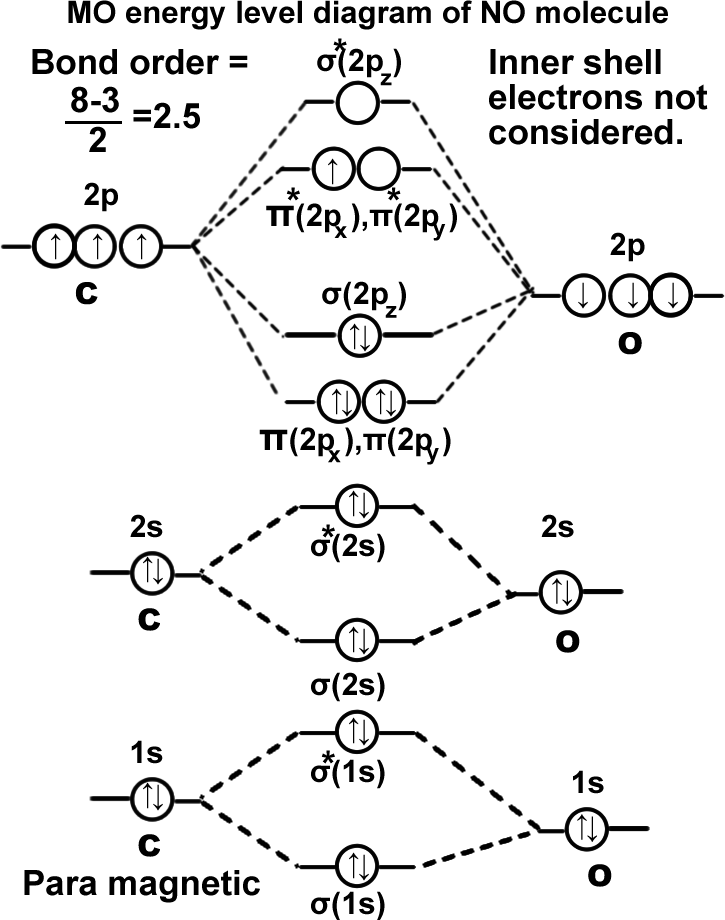
Nitric oxide molecule. (NO).

σ(1s²),σ^*(1s²),σ(2s²),σ^*(2s²), π(2p_x²)=π(2p_y²), σ(2p_z²), π^* (2p_x¹)=π^* (2p_y⁰),. It can be written as KK σ(2s²),σ^*(2s²), π(2p_x²)=π(2p_y²), σ(2p_z²), π^* (2p_x¹)=π^* (2p_y⁰). Molecule exists.

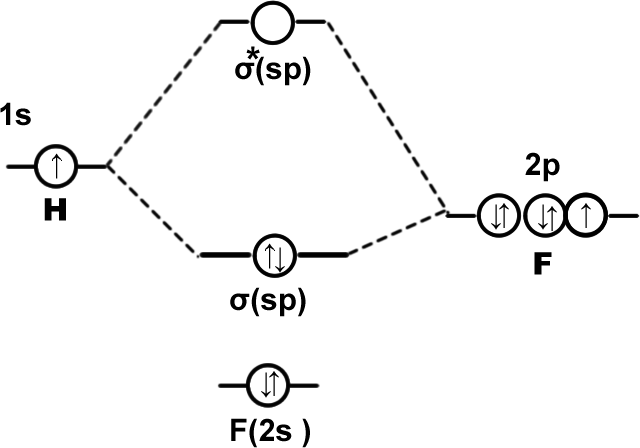
HF molecule: K(2s²),σ(sp)²,(2p_x²)(2p_y²).

Comparison Between Valence Bond Theory (VBT) and Molecular Orbital Theory (MOT) Common Features. Valence bond and molecular orbital theories have following features in common.

1. The basic principles involved in the distribution of electrons are similar. Thus, an orbital, whether atomic or molecular, cannot have more than two electrons. They are filled in the order of increasing energy. If there are more than one vacant orbitals having the same energy, they would first be filled singly.

2. In normal covalent bond formation, the essential interaction, according to both the theories, is the sharing of the bonding electron density by both nuclei and concentration of electron density between the nuclei.

In bond formation, orbitals to the bonded atoms, whether atomic or molecular, must overlap and have appropriate symmetry about the molecular axis.

Differences:

1. While VBT starts with individual atoms and con siders the interaction between them, MOT starts with the nuclei of the constituent atoms.

2. The wave function in VBT differs from that in MOT in-as-far as the latter does not involve the ionic terms in the total wave function.

3.VBT fails to explain the paramagnetic character of Oxygen molecule while MOT explains satisfactorily.

4. Resonance plays an important role in VBT. It has no place in MOT.

Orbitals which are left unchanged by the operation of inversion (are symmetric) are labelled with a subscript g, while those which undergo a change in sign (are antisymmetric) are labelled u. The symbols g and u come from the German words “gerade” and “ungerade” meaning “even” and “odd” respectively.