MOLECULAR ORBITAL THEORY (MOT) or M.O. Theory.
The molecular orbital theory was developed by Hund and Mulliken, later developed by Lennard Jones and Coulson. There is a saying that when they tried to explain the paramagnetic nature of oxygen molecule this theory originated. It is The basic question that arises in every one is when molecule is formed what changes takes place in the electrons and nuclei of the atoms participated. It is because the molecule has different properties compared to those of participant atoms. That means it must have its own electronic arrangement and position of nuclei. If only participating electrons are involved why should all properties change?.
According to the molecular orbital theory, which is modern and more rational, a molecule is considered to be quite different from the constituent atoms. All the electrons belonging to the atoms constituting a molecule are considered to be moving along the entire molecule under the influence of all the nuclei. Thus, a molecule is supposed to have orbitals of varying energy levels in the same way as an isolated atom has. These orbitals are called molecular orbitals. Molecular orbital is polycentric.
The molecular orbitals are filled in the same way as the atomic orbitals, following the ‘aufbau’ and Pauli exclusion principles. Thus, a molecular orbital, like an atomic orbital, can contain a maximum number of two electrons and the two electrons have opposite spins.
The difference between an atomic orbital and a molecular orbital is that while an electron in an atomic orbital is influenced by one positive nucleus, an electron in a molecular orbital is influenced by two or more nuclei depending upon the number of atoms contained in a molecule. According to wave mechanics, the atomic orbitals can be expressed by wave functions (Ψ),which represent the amplitude of waves.
According to M.O. theory, the molecular orbitals are formed by the linear combination of atomic orbitals(L.C.A.O) of the atoms which form the molecule. Those orbitals must have nearly equal or energies and proper symmetry.
For example, consider a hydrogen molecule consisting of two atoms labeled as HA and HB. Let the wave functions for the electrons in the atomic orbitals of two atoms A and B is ΨA and ΨB, respectively. When these atomic orbitals are brought closer, they combine to form molecular orbitals. The wave function Ψ for electron in the field of nuclei of atoms A and B (i.e, corresponding to the molecular orbital) may be written as a suitable linear combination of wave functions ΨA and ΨB. As discussed earlier, may be expressed in two ways.
Ψ= ΨA + ΨB and Ψ* = ΨA – ΨB
Where Ψcorresponds to wave function for symmetric combination whereas Ψ* corresponds to wave function for antisymmetric combination.
Now Ψ2 and (Ψ*)2 give probabilities of finding electrons in the two molecular orbitals formed according to the equations shown below respectively.
Ψ2 = (ΨA + ΨB)2 = ΨA2 + ΨB2 + 2 ΨA ΨB
(Ψ*)2 = ΨA2 + ΨB2 – 2 ΨA ΨB
It is evident that Ψ2 is greater that ΨA2 + ΨB2 by an amount equal to2 ΨA ΨB. That means the probability of locating electron is greater than either of the atomic orbitals ΨA and ΨB. That is it has lower energy than either of the atomic orbitals. This leads to stable bond formation. B.M.O (σ).
During the formation of BMO, the two electron waves of the bonding atoms reinforce each other due to constructive interference. High electron density between the nuclei which minimize repulsion and holds them together.
During the formation of ABMO, the electron waves cancel each other due to destructive interference. Least electron density between the nuclei.
That means the molecular orbital formed by symmetric combination of orbitals is more stable and is termed as bonding molecular orbital (σ). The other is antisymmetric combination of orbitals and is termed as antibonding molecular orbital (σ*).
The physical picture of these two types of MOS can be shown with, a simple case of combination of ls orbital of one hydrogen atom with 1s orbital of another hydrogen atom.
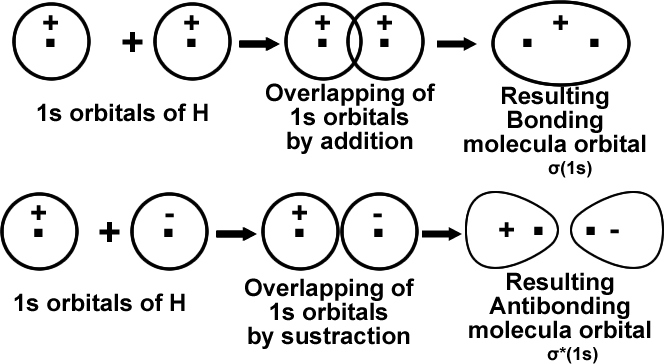
Molecular orbitals from ‘2s’ Atomic orbitals: just like the combination of ‘1s’ atomic orbitals, ‘2s’ atomic orbitals also combine in two ways to form ‘σ(2s)’bonding M.O and ‘σ*(2s)’ A.B.M.O.
Combination of p-atomic orbitals: There are
