ATOMIC STRUCTURE

SCIENTISTS AND THEIR DISCOVERIES:

1858 Plucker : Experiments with discharge tube.

1876 Goldstain : Gave the name cathode rays.

1879 Crookes : Found cathode rays have mass.

1891 Jhonson Stoney : Gave the name electron.

1895 Jean Perrin : Proved Cathode rays have -ve charge.

1897 J. J. Thomson : Found e/m ratio of cathode rays constant.

1895 W.C. Rontgen : Discovered x-rays.

1909 Millikan : Determined charge of electrons by Oil drop method.

1886 Goldstain : Discovered +ve rays.

1911 Rutherford : Discovered Nucleus and protons

1932 Chadwick : : Discovered Neutrons

1935 Yukawa : Discovered Meson (∏)

1932 C.D., Anderson : Discovered Positron

1927 Pauli : Discovered Neutrino

1955 Segre : Antiproton

1900 Max Planck : Quantum Theory

1903 Einstein : Modified Planck’s theory

1913 Niels Bohr : Structure of ‘H’ atom

1924 Louis-Victor de Broglie : proposed wave nature to electron.

1927 Heisenberg : Uncertainty Principle.

1912 Moseley : At.No. By studying x-ray frequency

1926 Schrodinger : Wave Mechanical concept.

1927 Hund : Rule of multiplicity.

Davison & Germer : Experimentally proved the wave nature of electron.

Bohr & Bury : Gave rules for filling electrons.

1995 Henry Becquerel : Discovered Radio Activity

1898 Madam Curie and Pierre Curie : Discovered Ra & Po

1911 Rutherford : Discovered Artificial disintegration.

: Discovered & & rays and studied the properties of α. β & ϒ

1900 P. Villard : Discovered ϒ-rays.

1942 Fermi : world’s first Nuclear reactor.

STATISTICS

e/m of cathode rays : 1.76 x 10¹¹ coulombs/kg or 5.28×10¹⁷ e.s.u/gm

Charge of electron : -1.602 x 10^-19 coulombs or -4.808 x 10^-10esu.

= 1 unit electricity or 4.808 x 10^-10 e.s.u.

Rest mass of electron : 9.12 x 10^-31 kg. Or 0.0005486 amu. 1/1837^th part of H-atom.

Classical electron radius : 2.8 x 10^-13 cms.

Density of electron : 2.17 x 10¹⁷ g/cc

Charge of 1 mole of electron : 96500 coulombs = 1 Faraday = 2.86 x 10¹⁴ esu.

Mass of 1 mole of electron : 0.55 mg. = 55 x 10^-4 gms. = 3.304 x 10²⁰ amu.

Average mass of H Atom : 1.675 x 10^-24 gms.

Mass of Proton : 1.6725 x 10^-27 kg or 1.00758 amu.

Gold foil used by Rutherford : 100nm thickness.

Charge of α-rays : 3.2 x 10^-19 coulombs.

Mass of α-rays : 6.6 x 10^-24 gms.

Mass of Neutron : 1.675 x 10^-27 kg or 1.00893 amu.

Neutron is 0.18% heavier than proton.

Mass of electron : 1/1837^th of H atom.

e/m of proton : 9.574 x 10⁴ c/gm

Positron e⁺ or +1e⁰ : Mass equal to electron with +ve charge.

Density of Neutron : 1.5 x 10¹⁴ g/cc

Meson (∏) : charge +1, 0 or -1

mass more than electron but less than proton.

Neutrino : No charge. Mass less than electron

Antiproton _-1P¹ or P^– : Mass equal to proton but -ve chage

Planck’s constant ‘h’ : 6.624 x 10^-27erg secs.

EQUATIONS

E = hƲ : Planck’s equation

Radius of the orbit = ‘r’ : 

Energy of the orbit = ‘E’ : 

Rydberg’s Constant = ‘R’ : = 109678 cm^-1 or 1.09678 x 10⁵ cm^-1

Bohr’s equation : ῡ = R [1/n₁² – 1/n₂²]

ῡ = Wave number of spectral line

n₁= Lower orbit, n₂=higher orbit

λ = = Debroglie ‘Equation

Heisenberg’s equation =      Δx = uncertainty in position & Δv = uncertainty in velocity.

lev = 1.602 x 10^-19 J

10⁶ev = 1Mev

10⁹ ev = 1Gev

An atom is represented _zX^A

where A= mass number(number of protons and neutrons).

Z= atomic number (number of electrons = number of protons). Atom is neutral.

ATOMIC STRUCTURE

1. Conditions for electric discharge in discharge tube are high voltage and low pressure.

2. Electric discharge starts at 10mm and below 0.01 mm – no discharge.

3. Alternate light and dark bands obtained in discharge tube are called STRIATIONS

dark spaces are called Crook’s dark spaces or Faraday’s dark spaces.

4. At 0.01 mm pressure the entire discharge tube will be filled with dark space and walls opposite to cathode give a greenish glow which is called Fluorescence.

5. Whenever a particle or radiation penetrate through Zinc sulphide or Barium Platinocyanide Ba(Pt(CN)₆) green coloured light spots are produced which are called SCIENTILLATIONS.

6. Cathode rays are so called because they are initially obtained from the material used as Cathode. After coming from the cathode they ionise the gases and thereby the intensity of cathode rays increases.

7. Properties of cathode rays:

a) They move in straight line. They cast shadows of the opaque object kept in their path.

b) They rotate the paddle wheel kept in their path which proves they have mass.

c) They heat the metal plate kept in their path due to continuous collisions.

d) They are deflected by electric and magnetic fields.

e) They are -vely charged.

f) The e/m ratio of cathode rays is constant irrespective of the gas and material used as cathode.

NOTE: J. J. Thomson discovered the e/m ratio of cathode rays by studying their deflection

in E and M fields.

e/m ratio of cathode rays was found to be constant. It proves that all substances have same kind of electrons and so electrons are common constituents of all atoms. This important conclusion is made by J. J. Thomson so the Credit of finding electrons is given to him.

e/m ratio is called specific charge.

g) When cathode rays fall on a metal plate (kept at 45°) X-rays are produced.

h) Cathode rays ionise gases.

i) They cause scintillations on ZnS or Ba [Pt(CN) ₆]

8. Some more important points about electrons:

a) Mass of electron was not determined; it was calculated from the values of ‘e’ and e/m. It is called Rest Mass.

b) Actual mass of electron ( m’) depends upon its velocity

m’ = Where m = Rest mass of electron, m’ = actual mass of electron, V = velocity of electron and C = Velocity of light

c) If velocity of electron is equal to that of light (V =C) mass tends to infinity.

Therefore as velocity of electron increases mass increases so e/m ratio decreases but charge remains same.

d) Millikan determined the charge of the electron by oil drop experiment.

Charge on the oil drops was always an integral multiple of 1.60 10^-19 C. That is q=ne. n=1,2,3….

Question: An oil drop has 8.0 x 10^–19C charge. How many electrons does this oil drop have?

We know q=ne that is n= q/e. Therefore n = (8.0 x 10^–19) / (1.602 x 10^-19 ) = 5.

e) Absorption of particle and emission of energy is called COMPTON EFFECT. The Principle in production of x-rays from cathode is the same.

f) Absorption of Energy and emission of particle is called Photo-electric effect.

Eg: Certain substances like Alkali metals emit electrons when light fall on them.

NOTE: The minimum amount of energy needed to remove a particle is called threshold energy and its frequency is called Threshold frequency.

g) β-rays emitted by radio-active substances are fast moving electrons.

9. Positive rays are discovered by Goldstein. He used a perforated cathode, so these are called

Canal rays. These are also called anode rays.

10. Anode rays are not emitted from anode but they are produced due to the ionisation of gas by cathode rays.

11. Like cathode rays they also travel in straight lines, deflected by electric and magnetic fields.

Produce scintillation etc.

12. e/m ratio of anode rays is not identical. It varies with the nature of gas and material used as cathode, which proves that all substances contain anode rays but they are not identical. It is always less than that of electron’s e/m value.

13. The name proton is suggested by Rutherford, Anode rays are not equal to protons but they contain protons.

14. When one or more electrons are removed from atom, the remaining positive residue with less electrons, more protons and neutrons is called anode particle.

15. When Hydrogen (protium) gas is taken in the discharge tube, the +ve particles obtained are called protons whose charge is exactly equal to electrons in magnitude but opposite in sign. Hence they are considered to be present in all atoms.

e/m ratio of anode rays is maximum when Hydrogen gas is taken in the discharge tube, because mass of protium is least. e/m of protons is 9.58 × 10⁷ C/Kg

16. J.J. Thomson proposed a hurried model of atom. It is compared with water melon. Every electron surrounded by a proton, but it failed.

17. Rutherford performed α-rays scattering experiment and discovered nucleus.

18. Gold-foil used by Rutherford has 0.00004cms thickness.

19. Observations and conclusions of Rutherford’s model atom.

a) Most of the α-rays passed through the metal foil, so Atom has large empty space.

b) Some of the α – rays are deflected and very few are repelled back which proves that the entire +ve charge of the atom is concentrated in a particular region called nucleus.

c) Atom contains some neutral particles in addition to pro tons in nucleus.

d) Rutherford estimated the radius of nucleus as 10^-12 cms and radius of atom as 10^-8cms.

e) 19. Rutherford model of atom is called planetary model or solar model.

20. Neutral particles guessed by Rutherford were discovered by Chadwick in 1932 as neutrons. He discovered them by bombarding ‘Be’ with α -particles.

21. Since protons and neutrons are present in nucleus they are called nucleons.

22. Electrons, protons and neutrons are called fundamental particles.

23. According to electromagnetic theory whenever a charged particle revolves around another charged particle, it should lose energy continuously. If it is so, the atom must emit energy continuously and that should lead to destruction. A continuous spectrum must be obtained. Neither of them is happening which proves atoms are not obeying electromagnetic theory.

24. The defect in Rutherford’s model atom is – He was unable to explain why atoms are not obeying electromagnetic theory.

25. According to electromagnetic theory emission absorption and propagation of energy by any particle is continuous.

26. In 1900 Max Planck proved that emission and absorption of energy by any particle is discontinuous i.e. whenever a sub stance absorbs or emits energy, it does so in fixed packets called quanta (hƲ)

27. Energy of quanta E = h Ʋ, where Ʋ= frequency of radiation.

E = hƲ (h is called Planck’s constant)

28. In 1903 Einstein modified Planck’s theory as follows: “Emission, absorption, and propagation of energy is discontinuous”, so Planck and Einstein together disproved e.m. theory.

29. Making use of Planck’s quantum theory Niels Bohr, in 1913 rectified the defects in Rutherford’s model atom.

30. Postulates of Bohr’s theory:

a) In every atom, around the nucleus, there are certain fix ed stationary energy levels called orbits in which electrons are revolving.

NOTE: This postulate means that energy of the orbit and electron are constant. It also means that the path of the electron is constant. This postulate says orbits are circular.

b) As long as electron revolves in a particular orbit it neither looses nor gains energy.

c) Because orbits are stationary, the energy difference is fixed, whenever electron gains energy or looses it should do so in fixed quantities.

En₂-En₁ = hƲ

En ₂ = Energy of higher orbit.

En₁ = Energy of lower orbit.

d) Anglar momentum of electron is an integral multiple of h/2∏.

mvr = (Note: This postulate is independently proposed by Bohr.)

31. According to Bohr the condition for the electron to revolve around the nucleus is

Centrifugal force = Centripetal force.

= where Z = At.number.

For H atom z = 1. Then =

32. Bohr derived an expression for the energy of the orbit in H atom.

E = – 

Where m = Rest mass of electron.

e = charge of electron

n = No. of the orbit.

NOTE: -ve sign indicates that PE of the electron decreases when it has come from infinity into the fold of nucleus.

On substituting all the values, the above equation becomes E = K.Cals/mole

E = ergs/atom. E = ev/atom.

E₁ = -313.6 K.Cals/mole, E₂ = -78.4 K.Cals/mole, E₃ = -34.8 K.Cals/mole, E₄ = -19.8 K.Cals/mole ….

As the No. of the orbit increases energy of the orbit increases, but the energy difference between orbits decreases.

33. Bohr derived en expression to calculate the radius of the orbit

r = = 0.529A^o where n = number of orbit and Z= atomic number.

As ‘n’ increases radius of the orbit also increases.

2∏r = nλ. Where 2∏r is formula for circumference of orbit and λ = wave length.

Hence, from the above equation the circumference of the Bohr’s orbit for the hydrogen atom is an integral multiple of de Broglie’s wavelength associated with the electron revolving around the orbit.

Circumference of first orbit = 3.4.A^o.

1A^o = 10^-8cms. 1nm = 10^-9m = 10^-7cms.

Velocity of electron is calculated as follows.

According to Bhor mvr = that is v =

Substituting ‘r’ formula v= that means v ∝

Velocity of electron in first orbit = 2.19×10⁸cms/sec.

34. Electromagnetic radiation is that which contain 2 components electric and magnetic which are perpendicular to each other and also perpendicular to the path of propagation of light.

E² = H² + M²

E=Energy of electromagnetic radiation.

H = Amplitude of Electric wave.

M = Amplitude of Magnetic wave.

35. em radiations are of different types.

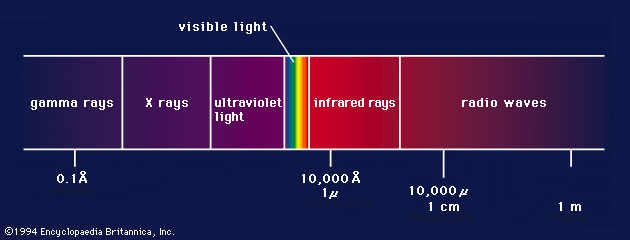
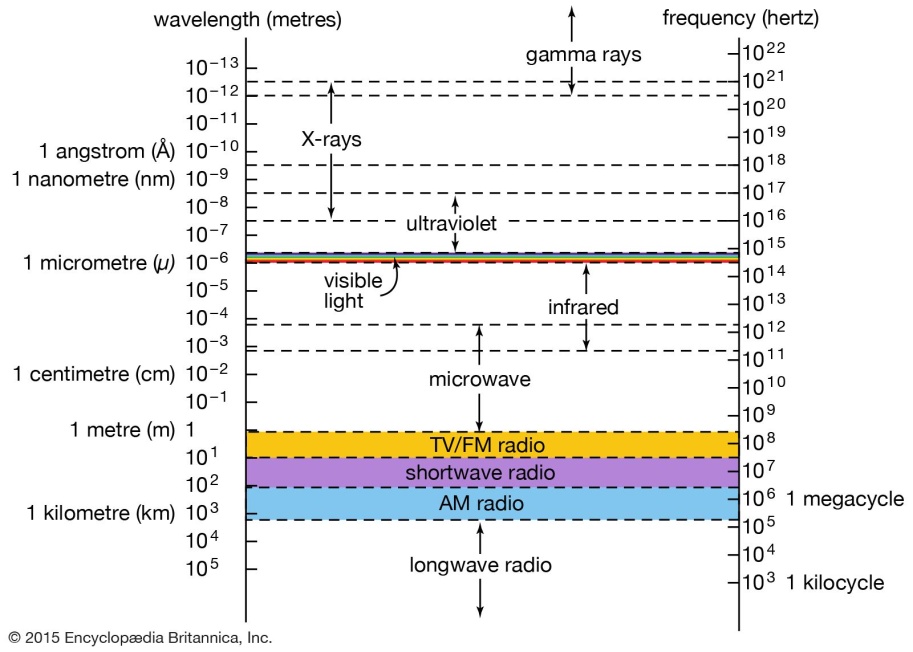
From gamma to radio waves wave length ↑ frequency Energy ↓

36. Any kind of e.m radiation is termed as light.

All e.m radiations are assumed to have a velocity of 3 x 10¹⁰ cms/scc.

Some important symbols and their units in wave nature:

Frequency (ν): The number of waves that pass through a given point in one second is called frequency.

Units: The SI units are cycles per second.  One hertz is the same as one cycle per second.

ν =C/λ. Where C= velocity of light and λ = wave length.

Wave number( ): The number of wave lengths per unit length or reciprocal of wave length.

= . it can also be written as ν =C. .

Amplitude (a): The height of the crest or depth of the trough of a wave is called amplitude.

Units: m, cm,pm.

Amplitude is a measure of the intensity or brightness of a beam of light.

Velocity (C):The distance travelled by a wave in one second is called its velocity.

Units: m/sec or cm/sec.

37. There are two theories regarding light –

a) Particle or corpuscular theory which is proposed by Newton and proved by the properties photoelectric and Compton effects.

b) Wave nature: It is proposed by Huygens and proved by the properties, interference and diffraction.

38. Light has dual behavior (both particle and wave nature)

39. The difference between the different e.m radiations is wave length. There is no clear demarcation because one diffuses into other.

40. Spectrometer is an instrument which resolves the radiations that are entering into it. (i.e.) it tells us radiations of how many wave lengths are entering into it.

41. If radiations of only two wave lengths enter into spectrometer only two lines are observed.

NOTE: Lines or groups of lines observed in spectrometer are called spectral lines and they are together called SPECTRUM. Each line indicates radiation of a particular wave length.

42. When white light is passed through spectrometer a continuous band of seven colours are obtained in visible region. That is it contains radiations of all wave-lengths in visible region. Such a spectrum which contains radiations of all wave lengths in a particular region is called continuous spectrum.

43. If a spectrum contains only lines corresponding to certain wavelengths that is said to be discontinuous spectrum.

44. When energy is supplied to Sodium Vapour electrons will absorb energy and excite to higher level while returning to their normal level they emit energy which when passed through spectrometer produce discontinuous spectrum. It has only two lines in yellow region corresponding to wave lengths 5890 and 5896 A⁰. It is called emission spectrum of Sodium. It is discontinuous.

45. Emission spectrum of elements is called atomic spectra or line spectra. It is characteristic of atoms of elements. No. two elements will have same line spectra.

46. Emission spectrum of compounds contains groups of lines. It is called band spectrum or molecular spectrum.

47. When white light is passed through spectrometer after passing through sodium vapour, we observe two lines are missing corresponding to wave length 5890 & 5896A⁰, that is those two radiations are absorbed by Sodium. It is called absorption spectrum of Sodium.

48. Like Emission spectrum, absorption spectrum is also characteristic of elements and compounds. The only difference is in emission spectrum. We see bright lines and in the latter we see dark lines. Both are discontinuous.

49. Emission spectrum is obtained when excited electron returns from higher level to lower level.

50. Absorption spectrum is obtained when electron excites to higher level.

51. Linear momentum is the product of mass(m) and linear velocity(v).

52. Angular momentum is the product of momentum of inertia (I) and angular velocity (ω).

For an electron of mass m_e, moving in a circular path of radius r around the nucleus the angular momentum = I ω.

We know I = m_e.r², and ω = where v= linear velocity.

Therefore angular momentum = m_e.r² = m_evr.

53. The angular momentum of an electron in a given stationary state can be expressed as follows.

m_evr = n where n = 1,2,3……..

54. Hydrogen spectrum: It is emission spectrum of Hydrogen. It contains 5 series.

a) Lyman Series: U. V. Region, observed by Lyman. It is due to return of some of the excited electrons directly to first level.

b) Balmer series: Visible region observed by Balmer. It is due to return of some of the excited electrons directly to 2nd level.

c) Paschen series: I.R. region observed by Paschen. It is due to return of some of the excited electrons direct y to 3rd level

a) Brackett Series: F. I. R. Region observed by Brackett. It is due to return of some of the excited electrons directly to 4th level.

e) Pfund series: F.F.I.R. Region observed by Pfund. It is due to the return of some of the excited electrons directly to 5th level.

52. To calculate the wave number of every line in Hydrogen spectrum Bohr used an expression.

ῡ = R[ – ]. This equation is actually proposed by Rydberg.

Where R = Rydberg constant =

and n₁= Lower level. n₂ = higher level

For Lyman series n₁ = 1 n₂ = 2,3,4……

Balmer series n₁ = 2 n₂ = 3,4,5……

Paschen series n₁ = 3 n₂ = 4,5,6……

Brackett series n₁ = 4 n₂ = 5,6,7……

Pfund series n₁ = 5 n₂ = 6,7,8……

Defects in Bohr’s theory:

(i) It is applicable to 1 eletron system. i.e. H and H like He⁺ , Li⁺² …..

(ii) If fails to explain Fine spectrum

(iii) Splitting of spectral lines in M, field in called Zeeman Effect. Splitting of spectral lines in E field is called Stark Effect. Bohr fails for explain both.

(iv) Stationary path for electron proposed by Bohr is proved to be wrong by Heisenberg.

1. To explain the existance of extra spectral lines (fine spectrum) Sommerfeld suggested Elliptical orbits in addition to circular orbits proposed by Bohr. According to him in every orbit there will be 1 circular orbit and (n-1) elliptical orbits (where ‘n’ is the number of the orbit).

In 1st orbit 1 circular orbit and no elliptical orbit.

In 2nd orbit 1 circular orbit and 1 ellipitcal corbit.

In 3rd orbit 1 circular orbit and 2 elliptical orbits.

In 4th orbit 1 circular orbit and (n-1) = 3 elliptical orbits.

NOTE: In an elliptical orbit nucleus will be present at one of the foci. However this theory fails to explain Zeeman & Stark Effects.

2. In 1924 Louis de Broglie proposed that every moving object(matter) has duel nature. He derived an expression for wave length of the moving object.

Wave length λ = that means λ = since momentum =mu.

Where m = rest mass of object in gms and u = velocity in cms/sec.

Electron being a moving particle will have wave nature also.

The wave nature of electrons was experimentally proved Davisson and Germer.

NOTE: Wave nature is more for lighter objects than for heavierobjects.

3. In 1927 Heisenberg proposed that it is not possible to find out the position and momentum of an (moving) object simultaneously (i.e.) there is uncertainty in position (Δx) and uncertainty in momentum ( Δmu). Therefore the position and momentum of an electron ‘can’t be found together accurately.

Therefore Δx . mΔu or Δx . Δu .

That means product of uncertainty is inversely proportional to mass.

Note: Uncertainty is more for lighter objects (like electrons) rather than heavier objects.

According to Heisenberg electron in an atom can be at any distance from the nucleus. Hence this theory disproves Bohr’s theory of stationary path for electron.

4. ORBITAL: An orbital is a three dimensional region in space where there is maximum probability of finding electron.

Erwin Schrödinger making use of Bohr’s concept of stationary energy levels, Louis de Broglie concept of dual nature and Heisenberg’s uncertainty principle proposed wave mechanical concept and derived an expression which is called wave equation.

Schrödinger wave equation indicates the variation of the value of Ψ value along x,y and z axes. Ψ is the amplitude of the wave function. denotes the particle density when applied to particles.

For an electron denotes the the probability of finding it in space at a given point.

Wave mechanical concept gave birth to 3 quantum Nos. Principle, Azimuthal and magnetic. A fourth quantum No. called spin quantum number is obtained from spectral study. These four quantum numbers, describe electron completely in the atom.

According to Schrödinger is directly proportional to probability of electron. Ψ is called wave function, or amplitude of electron wave. Schrödinger equation is the following.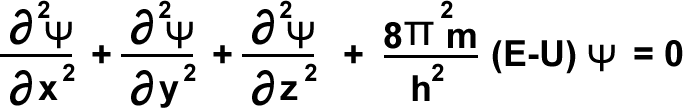

Ψ = wave function . m=mass of electron. E = Total energy of electron. U = potential energy of electron.

∇²Ψ + (E-v)Ψ = 0 where .

Ψ = EΨ where is a mathematical operator called Hamiltonian operator.

= V – [ + +]

Important features of the Quantum Mechanical Model of Atom:

a) It states that the energy of electron in an atom is quantized.

b) It explains the probability of finding the electron around the nucleus in three dimensionally.

c) An atomic orbital is the wave function Ψ for an electron in an atom.

d) Significance of ψ : It is a wave function.It corresponds to energy state which contains all information about electron.

e) Significance ofψ2 : It is a probability function. It indicates maximum probability of finding an electron at a certain point in an atom.

f) The probability of finding an electron at a certain distance from the nucleus is called radial probability.

g) The curves obtained by plotting probability function D = 4πr² d rΨ² and radial distance (r) are called

radial probability distribution curves.

h) Number of peaks obtained in a curve = (n – l) where n = principal quantum number and l = Azimuthal quantum number.

i) The nodal surface of 2s orbital exists at a distance of 2a₀ from the nucleus. Where a₀ is the Bohr

radius (0.529A⁰).

j) The curve for 2s orbital has two peaks the curve passes through lower maximum at 0.53 A⁰ and higher maximum at 2.6A⁰ radial distance.

Quantum Numbers:

1. Principle Q.No: It is proposed by Bohr and is denoted by the letter ‘n’. it will have only +ve integral values n = 1,2,3,4…etc. The values of ‘n’ are also represented in letters n = K, L, M, N… ). Each value of Principle .No. indicates an energy level and it also indicates the size of the orbit.

Principle Q.No. value of an electron indicates in which orbit it is present and what is its total energy. As the value of ‘n’ increases the distance of electron/orbital from the nucleus increases and energy also increases.

2. Azimuthal Q.No. (or) Secondary Q.No. (or) Subsideary, Q.No. (or). Angular Momentum Q.No..

It is proposed by Sommerfeld and represented by the letter ‘l’. It will have values 0 to (n-1). Each value of indicates a sub energy level.

n = 1 l =o 1st orbit has only 1 sub-orbit 1s

n=2 l = 0,1 2nd orbit has 2 sub-orbits 2s and 2p

n = 3 l = 0, 1, 2 3rd orbit has 3 sub-orbits 3s, 3p & 3d

n = 4 l= 0,1,2,3 4th orbit has 4 sub-orbits 4s, 4p, 4d & 4f

a) No. of the orbit = No. of sub orbits present in it. This Q .No. explains Fine spectrum (division of spectral lines)

b) This Q.No. value of an electron indicates in which sub-orbit electron is present and what is the energy possessed by it due to angular momentum, hence it is called angular momentum Q.No.

d) This Q.No. explains the shape of the sub-orbit.

S – Spherical. P-dump-bell. d-double dump-bell. f – Shape not known.

e) Values for s,p,d & f sub-orbits are 0.1.2.3 respectively.

3. Magnetic .No: It is denoted by the letter ‘m’ or ‘ml’. It was proposed by Lande to account Zeeman effect. It will have values ‘-l’ to 0 to ’+l, each value of ‘m’ indicates an orbital. Values of ‘m’ for a particular sub-orbit indicate its orientation in space when kept in magnetic field.

l= 0 m = 0 (S-Suborbit has 1 orbital).

l = 1 m = -1, 0, +1 (p-suborbit has 3 orbitals)

1 = 2 m = -2,-1,0, +1, +2 (d-suborbit has 5 orbitals)

L =3 m = -3, -2, -1-0 +1, +2, +3 (f-suborbit has 7 orbitals)

The +ve and –ve signs indicate only change in direction but the magnetic quantum number as such is neither positive nor negative.

a) Magnetic Q.No.value of an electron indicates in which orbital it is present.

Number of orbitals in a sub-orbit= (21+1)

b) This Q.No.explains Zceman effect. ‘m’ value of an electron indicates the magnetism associated with the electron.

4. Spin Q.No: It was proposed by Uhlenbeck and Goudsmit .It is denoted by ‘s or ms’. Every electron will spin around its on axis while revolving round the nucleus. ‘s’ will have values + or – .

[↑ ] Clock wise spin is denoted like this.

[↓] Anticlockwise is denoted like this.

Spin Q.NO. Value of an electron indicates its spin with respect to an axis.

Spin angular momentum of the electron = where s = total spin.

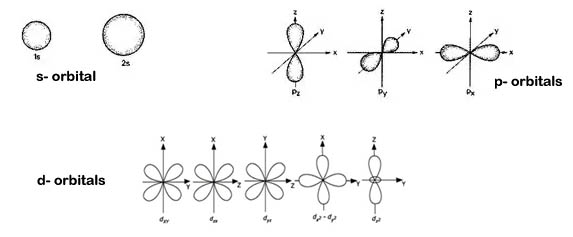
Shapes of sub-orbits:

Note:

(i). All‘d’ orbitals have same energy. They are called degenerate orbitals.

(ii). d_xy , d_yz and d_xz orbitals are known as non-axial d orbitals because the lobes of the orbitals are not available along the axis.

(iii). –, and are known as axial d-orbitals because the lobes of the orbitals are along the axis.

The probability of finding an electron within the radial space around the nucleus is called radial probability distribution.

The radial probability distribution of electron can be calculated by 4∏r²drΨ².

Angular probability of finding an electron within the radial space around the nucleus is called atomic orbital.

Probability of finding an electron in the nucleus is zero. The plane where Probability of finding an electron is zero is called ‘nodal plane. For‘s’ orbital there is no nodal plane. For ‘p_x’ nodal plane is yz. For ‘p_y’ nodal plane is xz. For ‘p_z’ nodal plane is xy.

5. Pauli’s Exclusion principle: “No two electrons in an atom Can have all the four Q.Nos. Identical”. This principle indicates the maximum number of electrons that can be present in an orbit sub-orbit and an orbital

The maximum No. of electrons in any orbit = 2n²

The maximum No. of electrons in any sub-orbit = 2(2l+1)

The maximum No. of electrons in any orbital = 2

Eg. 1st orbit-2, 2nd orbit-8, 3rd orbit-18 s-sub-orbit-2, p-sub-orbit-6, d-sub-orbit-10, f-sub-orbit-14.

Energies of sub-orbits:

(1) In any sub orbit energy of s<p<d<f. (2) Energy of ns ≈(n-1) d. eg: 4s≈ 3d

(3) Energy of (n-1)d ≈ (n-2) f, eg: 6d ≈ 5f

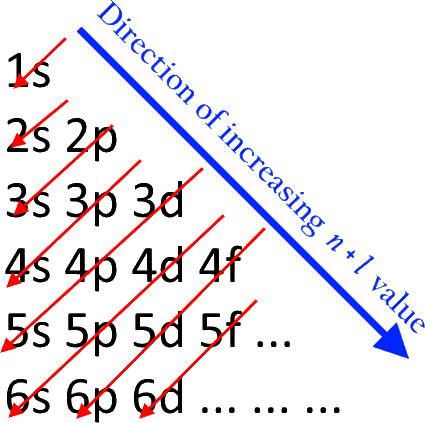
6. Rules for filling electrons into sub orbits (Aufbau principle):

1) Electrons will enter into sub-orbits in the increasing order of their energy. it can be calculated using their (n+l) values.

2) Unless each orbital in a sub-orbit gets one electron, pairing will not take place in any orbital (Hund’s rules of Max. multiplicity).

Alternate explanation is, the filling of electrons in the degenerate orbitals will take place in such a way that the multiplicity (M) value will be maximum.

M = 2]s]+1. Where s=total spin value of all electrons in degenerate orbitals.

While filling the electrons in the degenerate orbitals the spin of the electron must be same that is either +1/2 or -1/2.

For example consider the nitrogen atom: the electronic distribution must be any one of the shown below.

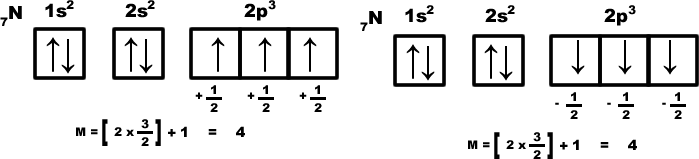
3) If two sub-orbits have equal (n+ l) value electron will enter into that sub-orbit whose ‘n’ value is less. Sub Eg: Among 3d & 4p electrons enters to 3d sub- orbit.

4) Elements with half-filled or completely filled sub-orbits are more stable.

Such electronic configuration is stable E.g. Cr. cu, etc.,

MOELLER DIAGRAM

Electronic configurations are written in ‘ nl^x ‘ method where’ n’ is the principal quantum number, ‘l’ is the azimuthal quantum number and ‘x’ is the number of electrons present in it.

5. The orbitals in a sub orbit having same energy are called degenerate orbitals.

6. When two electrons are paired with opposite spin coulombic repulsion energy is lowered.

Exceptions: After ‘6s’ level is filled 1 electron only enters to ‘ 5d ‘ level and remaining enters to ‘ 4f ‘ level. After ‘4f’ level is filled ‘5d’ start filling.

2) After ‘7s’ level is filled 1 electron only enters to ‘6d’ level and remaining enters to ‘5f’ level till it is filled, once it is filled 6d starts filling.

Some of the exceptions in the elements for which the electronic configurations does not follow the Aufbau principle are given below.

₂₄Cr : [Ar]4s¹3d⁵.

₄₂Mo : [Kr]5s¹4d⁵.

₄₁Nb : [Kr]5s¹4d⁴ .

₂₉Cu : [Ar]4s¹3d¹⁰.

₄₇Ag : [Kr]5s¹4d¹⁰.

₇₉ Au : [Xe]6s¹5d¹⁰.

₄₄Ru : [Kr]5s¹4d⁷ .

₄₅Rh : [Kr]5s¹4d⁸ .

₄₆Pd : [Kr]5s⁰4d¹⁰ .

₇₈Pt : [Xe]6s¹4f¹⁴5d⁹ .

₅₇La : [Xe]6s²5d¹4f⁰ .

₈₉Ac : [Rn]7s²6d¹5f⁰ .

₉₀Th : [Rn]7s²6d²5f⁰ .

Several exceptions can be explained on the basis of achieving half filled or completely filled configuration of a subshell which are relatively more stable. This can be explained as follows.

The symmetry leads to stability (as the rule of nature).

Without changing the configuration if an electron in a subshell can have exchanges then some of energy is released which is known as exchange energy. More number of exchanges causes more release of energy and that leads to more stability. The possible exchanges for ‘d⁵’ configuration is shown in the following figure. Total exchanges are ten.

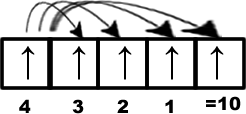
Similarly for a ‘d¹⁰’ configuration total number of possible exchanges will be 10+10 = 20. The two electrons involved in the exchange must have same spin.

7) Some important points in atomic structure:

1) Electrons, protons and neutrons are called fundamental particles.

2) Neutrons and protons are called nucleons since they are present in Nucleus.

3) Among fundamental particles neutron is relatively less stable because it can disintegrate.

Neutron = Proton+ electron + Neutrino.

4) When electron and positron combine a photon of light energy is emitted.

5. Isotopes are atoms of the same elements with same At.No. (No.of electrons and protons) but differing in the No. of neutrons i.e. they differ in mass No.

Examples: ₁₇Cl³⁵ and ₁₇Cl³⁷. ₈O¹⁶ and ₈O¹⁸ there is ₈O¹⁷ but least abundant. ₁₁Na²³ and ₁₁Na²⁴

Frederick Soddy was the one who discovered the isotopes in radioactive elements. Separation of isotopes is first done by Aston (Ne-20 and Ne-22).

Tin (Sn) has a maximum of 10 isotopes.

6. Atomic number is represented by the symbol Z. Z = No. of electrons = No. of protons.

7. Mass number is represented by the symbol ‘A’.

A = No. of protons + No. of Neutrons. That means A=Total No. of Nucleons.

A+Z = Total No. of fundamental particles.

8. At. Wt. of an element is average of mass number respective isotopes according to their relative abundance. That is why At Wts. usually have fractional values. Mass No. is characteristic of isotope and at. Wt. is characteristic of clement.

9. Isobars are Atoms of different elements having same mass number. They have same No. of nucleons. Example : ₁₉K ⁴⁰ ₂₀ Ca ⁴⁰ ₂₀Ar ⁴⁰ The term “isobars” (originally “isobares”) for nuclides was suggested by Alfred Walter Stewart in 1918.

10. Isotones are atoms of different elements with same number of neutrons. No. of Neutrons = A-Z. The examples are ₁₄Si³⁰ and ₁₅P³¹ both have ‘16’ neutrons.

11. At.Nos. of elements are found by Moseley by studying X-ray Frequency of elements. A graph plotted between At.Nos. & square root of X-ray frequency will be a straight line.

12. Species having same No. of electrons are called Iso-electronic. Example; C^4- N^3- and O^2- have ‘6’ electrons. Ne, Na⁺, Mg⁺² Al ⁺³ have 10 electrons. CO₂ and N₂O have 22 electrons are isoelectronic .  Any group of molecules or ions that have the electrons are Isosteres. Example: CO₂ and N₂O.

13. Isodiaphers are a set of nuclides that have a different number of protons and neutrons, but there is the same difference between the protons and neutrons. That means (n-p) = (A-2Z). For example uranium₉₂U ²³⁸ and thorium ₉₀Th ²³⁴have a difference of 54.

14. The energy possessed by atoms or molecules of a substance at the absolute zero (0⁰ A) temperature is called Zero point energy.

E ₀ per mole = . n₀ .hƲ. where Ʋ = vibration frequency.

E₀ per molecule = hƲ

15. 1 Mole of Photons is called Einstein.

16. No.of orbitals in an orbit = n².

17. When nucleus is formed from protons and neutrons some mass is lost which converts into energy. It is called binding energy. It is responsible to keep the nucleons together. If binding energy per nucleon is more stability of nucleus is more.

= Binding energy per Nucleon

Binding energy per nucleon in He nucleus is 7 M.E.v.

18. Besides protons and neutrons nucleus contains some other particles like positrons, meson, neutrino etc. these are called sub-atomic particles.

19. Meson theory was proposed by Yukawa to explain the stability of Nucleus. In the nucleus proton and Neutrons undergo continuous interchange due to charged Mesons. Thereby repulsions between protons are not concentrated hence nucleus is stable.

20. Sub-atomic particles are always not present in the nucleus, but they are formed in the nucleus when nucleus undergoes some change.

21. In Hydrogen atom(₁H¹) there is one electron and one proton so they are only attractions and no repulsions but other atoms have.

22. Nucleus containg same No.of neutrons and protons is stable. If the neutrons and protns are of even number still more stable.

23. If the two protons in H₂ molecule spin in the same direction it is called ortho H₂. If they spin in the opposite direction, it is called para H₂.

27. Bohr-Bury Rules: (a) An orbit cannot contain more than 2n² electrons (b) Last orbit cannot contain more than 8 electrons. (c) Penultimate orbit cannot have more than 18 electrons.

28. The magnetic properties of a substance can be determined by examining its electron configuration: If it has unpaired electrons, then the substance is paramagnetic and if all electrons are paired, the substance is then diamagnetic.  Ferromagnetic materials are strongly attracted to an external magnetic field.

29. Paramagnetic arises due to the presence of unpaired electrons. Diamagnetic arises due to presence of all paired electron.

If we assume that the magnetic moment arises entirely from unpaired electron spins, then the spin only magnetic moment value can be calculated using the following formula:

µ_s = BM

Where n is the number of unpaired electrons present in the species. Spin only magnetic moment is also

referred to as magnetic momentum for convenience sake

Let us predict the magnetic behaviour of ions based on their electronic configurations

For example, consider Mn²⁺, the electronic configuration is:

Mn: [Ar]3d⁵4s² .

Mn²⁺: [Ar]3d⁵. Five unpaired electrons are in ‘3d’.

Then µ_s = BM = 5.92BM.

30. Exchange energy is the energy released when two or more electrons with the same spin-exchange their positions in the degenerate orbitals of a sub shell.  When electrons of same spin are present in different orbital of same energy, these electrons tend to exchange among themselves. They are called exchange pair. This decreases the energy of atom. The decrease in energy due to exchange of electrons in orbital of same energy is called “exchange energy” This increases stability of atom. The more is the exchange possibility in an atom the more it is stable. For example 3d⁵4s¹ configuration for Chromium is more stable than 3d⁴4s² configuration.

31. Nodal planes of different orbitals.

Nodal plane is defined as the plane passing through nucleus, at which the probability of finding electrons present in that orbital is zero. The possible nodal planes for different subshells are as follows.

1. The number of nodal planes for ‘s’ orbital is zero.

2. ‘xy’ plane is the nodal plane for ‘p_x’ orbital, ‘xz’ plane is the nodal plane for orbital ‘p_y’ and ‘yz’ plane is the nodal plane for ‘p_z orbital.

3. ‘xz’ & ‘yz’ planes are the nodal planes for ‘d_xy’ orbital.

‘xz’ & ‘xy’ planes are the nodal planes for ‘d_yz’ orbital.

‘yz’ & ‘xy’ planes are the nodal planes for ‘d_xz’ orbital.

For d_x²_-y² orbital, planes perpendicular to xy-plane and inclined at 45⁰ and ‘x’ & ‘y’ axis are the nodal planes.

For ‘d_z² ‘ orbital there are no nodal planes but two nodal surfaces available.

32. In 1930 J.C.Slater suggested that every electron will be attracted by all protons In the nucleus and will be repelled by all other electrons. He established a simple relation for determining the net attraction on an electron. It is called effective nuclear charge on that specific electron (Z_eff).

Z_eff = (Z – σ) . Where Z= atomic number and ‘σ’ is the shielding constant which is the measure of net repulsion caused by other electrons in the same shell and inner shells.

33. Rules to calculate ‘σ’ value for an electron.

1. Write the electronic configuration following all the rules. Rearrange it according to orbit wise.

For example let us consider iron (Fe) atom. 1s²2s²2p⁶3s²3p⁶4s²3d⁶ is the configuration.

Now we have to rewrite it as (1s² ) (2s² ) (2p⁶) (3s²) (3p⁶ ) (3d⁶ ) (4s²).

2. For‘s’ and ‘p’ sub shell:

Electrons present right side of ( ) have no contribution to σ value.

Other electrons in the same subshell 0.35 value each( except for the electrons in ‘1s’ sub shell, that contribute 0.3).

For electrons in (n-1) shell 0.85 value each.

For electrons in (n-2) shell onwards 1.0 value each.

3. Rules for‘d’ or ‘f’ electrons:

Electrons present right side of ( ) have no contribution to σ value.

The value for electrons in same subshell ( ) is 0.35 each.

Rest of the electrons left to ( ) is 1.0 value each.

Example: let us consider ‘Fe’ atom. Fe ; [Ar] 4s²3d⁶.

According to Slater’s rules it needs to be written as follows.

(1s² ) (2s² ) (2p⁶) (3s²) (3p⁶ ) (3d⁶ ) (4s²).

‘σ’ value for ‘4s’ electron.

In the same subshell there is one electron = (1x 0.35) = 0.35.

In (n-1) subshells there are 14 electrons = (14 x 0.85) = 11.9.

In (n-2) subshells onwards there are 10 electrons = (10 x 1) = 10

Total = 22.25 = σ.

For ‘4s’ electron Z_eff = 26 – 22.25 = 3.75.

‘σ’ value for ‘3d’ electron.

In the same subshell there is one electron = (5x 0.35) = 1.75.

Other electrons left to ( ) are 18 = 18 x 1 = 18

Total = 19.75 = σ.

For ‘3d’ electron Z_eff = 26 – 19.75 = 6.25.

Example – 2:

Sc – 1s²2s²2p⁶3s²3p⁶4s²3d¹ . Now we have to rewrite it as (1s² ) (2s² ) (2p⁶) (3s²) (3p⁶ ) (3d¹) (4s²).

‘σ’ value for ‘4s’ electron = 1 x 0.35 + 9 x 0.85 + 10 x 1.0 =18. Therefore Z_eff =21 – 18 = 3.0.

‘σ’ value for ‘3d’ electron = 18 x 1.0 = 18. Therefore Z_eff =21 – 18 = 3.0.

As both ‘4s’ and ‘3d’ have same Z_eff we can conclude that removal of ‘4s’ electron takes place first. Actually we observe the same in reactions.

However another method is developed by Clementi and Raimondi which suggests that Z_eff is same for an electron in the same shell. I gave this information only to tell that some other people also worked in the same area which needs to be considered at higher levels of study.

34. Electronic configuration of ions.

1. For an anion;

A + e^-1 A^-1, and A^-1 +e^-1 A^-2.

If the atomic number of atom ‘A’ is ‘Z’, then total number of electrons in A^-1 = (Z+1) and in A^-2 = (Z+2).

Now fill the extra electrons added in the empty orbitals available in that element.

Example: Electronic configuration of N = 1s²2s²2p³. Remember the three electrons in the ‘2p’ sub shell have occupied one in each of the ‘2p’ orbitals and have same spin.

Now write the electronic configuration of N^-3 ion as 1s²2s²2p⁶. It means the three electrons will go to ‘2p’ orbitals and get paired.

2. For cation:

M – e^-1 M⁺¹, and M^-1 – e^-1 M^-2.

If the atomic number of atom ‘M’ is ‘Z’, then total number of electrons in M^+x = (Z-x), where ‘x’ is the number of electrons removed. If ‘M’ is an ‘s’ or ‘p’ block element write the electronic configuration following the normal rules.

Example:

Mg⁺² = 1s²2s²2p⁶. It means the two electrons in ‘3s’ level are removed.

Al⁺³ = 1s²2s²2p⁶. . It means the two electrons in ‘3s’ level and one electron of ‘3p’ level are removed.

If ‘M’ belongs to d-block or f-block, then first write the electronic configuration of ‘M’.

Remove ‘x’ number of electrons from ’ns’ then from (n-1)d and then from (n-2)f orbital gradually.

Example-1:

₂₆Fe = [Ar]3d⁶4s², that of Fe⁺² = [Ar]3d⁶, and that of Fe⁺³ = [Ar]3d⁵.

Example-2:

₂₉Cu = [Ar]3d¹⁰4s¹, that of Cu⁺¹ = [Ar]3d¹⁰ and that of Cu⁺² = [Ar]3d⁹.

Example-3: For ‘f’ block elements.

₆₄Gd = [Xe] 4f⁷5d¹6s².

Gd⁺² = [Xe] 4f⁷5d¹6s⁰,that of Gd⁺³ = [Xe] 4f⁷5d⁰6s⁰ and that of Gd⁺⁴ = [Xe] 4f⁶5d⁰6s⁰.

35. Magnitude of velocity of electron increases wit h increase of positive charge on the nucleus and decreases with increases of principle Quantum Number.

36. Number of revolutions per second (or) orbital frequency by an electron in a shell =   .

= = 6.66 x 10¹⁵ x (Z² / n³ )

37. Time period of revolution of electron in n^th orbirt (T_n) = (2πr)/V_n . it is equal to 1.5×10^-16 x (n²/Z²) sec.