CHEMICAL BONDING
1. The force of attraction that is binding, atoms or oppositely charged ions together is called chemical bonding.
2. There are two types of chemical bonding ionic and covalent bonding.
3. Electrovalency is proposed by Kossel and Covalency is proposed by Lewis.
4. Ionic bond is formed by the transfer of electrons from one atom to another. It is also called Electrovalent bond.
5. During Ionic bond formation the atom having low I.P, E.N and E.A. values will lose 1 or more electrons and other atom having more I.P, EN and EA values gain one or more electrons. The atom which lost electron or electrons will become cation and its size decreases. The other atom which gained will become anion and its size increases. In between anion and cation the electrostatic forces of attraction existing is called Ionic bonding. Ionic bonding is formed between the following elements generally. s1(1A)group elements & p4 (4A), s1(1A)group elements & p5(5A), s2(2A)group elements & p4 (4A), s2(2A)group elements & p5 (4A),
Transition metals and inners transition metals form only, covalent band in higher valency states. On lower state they form both covalent and ionic bonds.
6. Always unbonded atoms will have more energy than bonded atoms.
7. Electrovalency: The No. of electrons lost or gained by an atom during ionic bond formation is called its electrovalency. Eg: In NaCl electrovalency is +1 & -1 respectively. In Cao electrovalency is +2 & -2 respectively.
8. In the solids of ionic compounds there are no molecules. Every ion is surrounded by a group of oppositely charged ions, so every ion is connected to a group of oppositely charged ions. Hence ionic bonding is non-directional and non-rigid.
10. An orderly three dimensional arrangement of atoms, molecules or oppositely charged ions is called crystal lattice arrangement.
11 Crystals are of 4 types.
a) Ionic crystals: These contain oppositely charged ions arranged in an orderly 3 dimensional manner. The forces of attraction between them are strong electrostatic forces. Eg: NaCl, CsC1,KI ….
b) Molecular crystals: These contain molecules arranged in an orderly 3 dimensional manner. The forces of attraction between them are relatively weak Vander Waals Forces. Eg: Glucose, Urea etc.,
c) Covalent Crystals: These contain atoms which are connected to each other by covalent bonds and arranged in an orderly 3 dimensional manner. Eg: Diamond, graphite, carborundum (SiC), B4C3.
d) Metallic Crystals: These contain metal atoms which are arranged in an orderly 3 dimensional manner and the forces of attraction between them weak Electrostatic forces.
12. Hardness, density, M.P. & B.P of various crystals is as follows.
Covalent Crystals > Ionic Crystals > Metallic Crystals > Molecular Crystals.
13. Unit cell: In every crystal there is a smallest repeating unit which is called Unit cell.
Eg: 1. In NaCl every Na+1 is surrounded by 6 C1-1 ions and vice versa. The arrangement is Octahedral or Square bypyramid. Hence the shape of the unit cell is square bypyramid or Octahedral.
2. In CSC1 every ion is surrounded by 8 ions. Therefore the shape of unit cell is CUBE.
14. Coordination number: The number of species surrounding a particular species in crystal lattice arrangement is called coordination number of that species. It can be atom molecule or ion.
Eg: In NaCl coordination No. of Na+ or C1– is 6. In CSC1 coordination No. of Cs+ or C1– is 8.
15. Lattice point: In a crystal, the position of every atom, molecule or ion is called lattice point.
16. There are 230 ways of arranging lattice points. They give rise 14 shapes which are called BRAVIS LATTICES. These are condensed to 7 and they are called Basic Crystal Systems – (1) Cubic (2)Tetragonal (3) Orthorhombic (4) Rhombohedra (5) Monoclinic (6) Triclinic (7) Hexagonal.
17. Cubic Crystal lattice systems are of 3 types.
(a) Simple cube: Where lattice points are at 8 corners of cube.
(b) Face centered cubic lattice (F.C.C): Where lattice points are at the centre of faces. They can be at places also
(c) Body centered cubic lattice (B.C.C): Where lattice points are at 8 corners and one at the centre of body.
Eg: NaCl, KC1, KBr etc. are f.c.c. whereas CsCl,RbC1 etc are b.C.C.
18. Lattice energy (U): It is the amount of energy liberated when 1 mole of a crystal is formed from its gaseous atoms, molecules or oppositely charged ions.
19. Born-Haber cycle is used to calculate the Lattice energy.
20. Usually radius of cation will be less than radius of anion (exceptions RbF, CsF). The ratio between radius cation (rc) and anion (ra) is called Radius Ratio (R). R = rc/ra,
If R < 0.43 coordination number is 4.
If R> 0.43 and < 0.73 coordination number is 6.
If R > 0.73 coordination number is 8. It is called radius ratio effect. (However it is not rigid rule).
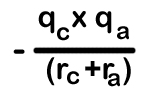21. Whenever two oppositely charged ions approach each other energy decreases. It is calculated as shown here.
The –ve sign indicates decrease of energy. Here qc and qa are magnitude of charges of cation and anion respectively.
22. If the magnitude of this value is more ‘U’ is more. Stability of crystal is more.
Eg: Among NaF, NaCl, NaBr & NaI, U decreases in the same order because’ rc ‘ is same but ‘ ra ‘ value is increasing.
Eg: NaF, KF, RbF & CaF, U decreases in the same order because radius of anion is same but radius of cation is increasing.
Eg: LiF and MgO have same ( rc + ra ) value but of MgO is more stable because magnitude of charge is more.
Eg: NaF and Cao have same ( rc + ra ) value but CaO is more stable because magnitude of charge is more.
23. Properties of Ionic compounds:
a) In ionic compounds there are no molecules instead there are ions each ion is surrounded by a group of opp. ions. The forces of attraction between them are strong electrostatic forces, which are very strong; hence they possess more M.P. and B.P. density and hardness ‘compared to covalent compounds.
b) In solids ions have no movement so they do not conduct electricity and heat. In molten state or in solutions they conduct electricity because ions get freedom of movement.
c) Capacity to weaken the electrostatic forces is called Dielectric constant. It is a measure of a substance’s ability to insulate charges from each other. Solvent having it is called polar solvent. Ionic compounds arc soluble in polar solvents. If polarity of the solvent is more solubility is more.
d) Ions in ionic compounds respond their tests only in molten state or in solutions because ions get movement.
e) When ionic compounds dissolve in water or any polar solvent two changes take place (i) crystal lattice breaks and ions gets separate by absorbing lattice energy (+U) (ii) Ions will be surrounded by solvent molecules liberating solvation energy (-s).
If U > S dissolution is endothermic and solubility is less.
If U < S dissolution is exothermic and solubility is more.
If the solvent is water S is called Hydration energy (H)
f) Ionic compounds do not exhibit isomerism because ionic bond is a non directional bond.
Covalent bond or electron pair bond:
24. Covalent bond is formed between atoms whose EN, EA and IP values are equal or nearly equal. It can be formed between Homo as well as Hetero atoms, whereas ionic bond will be formed only between Hetero atoms.
25. Covalent bond is formed by the sharing of 1 or more electron pairs.
26. Covalency is proposed by Lewis. According to him an atom enters into covalent bonding to attain 8 electrons in its valency shell. It is called Octet rule, Except H atom, which attains only doublet.
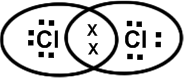
Each C1 atom attains 8 electrons and reaches ‘Ar’ configuration. These are called Lewis electron dot structures.
27. Valency Bond theory (V.B. Theory): It is proposed by Heitler and London and later on developed by Pauling and Slater. Since Pauling is the major contributor he is considered as Father of valence bond theory. V.B.Theory and Molecular orbital (MO) theory are based on quantum mechanical principle.
28. Important points in VB theory:
a) Pairing of unpaired electrons leads to bond formation.
b) Pairing of unpaired electrons takes place provided they have opposite spins.
c) Overlapping of atomic orbitals (AOs) with unpaired electrons and opp. spins leads to bond formation.
d) Strength of the bond depends upon the extent of over lapping. The more the overlapping, the stronger the bond formed.
e) Dative bond (coordinate bond) is formed by the overlapping of an orbital having a pair of electrons and a vacant orbital.
f) In a covalent between two atoms nucleus of each atom not only attracts its own electrons but also the electrons of other atom. That means there are attractive forces which tend to bring them closer. The electrons of the two atoms repel each other as a result there is repulsive forces which tend to push them apart.
29. Covalent bond is directional and rigid.
30. Whenever a covalent bond is formed between two atoms, electron density in between nuclei increases. Repulsion between nuclei decreases, attraction between nuclei and electron cloud increases, energy decreases and stability increases.
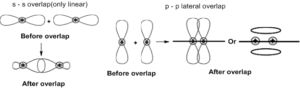
31. Atomic orbitals can overlap in two ways linear and lateral. Two s-orbitals always overlap linearly, one s-orbital and one p-orbital overlap only linearly. The bond formed is called ‘σ ‘bond. If there is only one bond between two atoms it is always ‘σ’ bond. ‘σ’ bond between ‘1s’ orbitals is exceptionally stronger.
Strength of the bonds follows the order: ‘σ’ p-p > ‘σ’ s-p > ‘σ’ s-s.
32. Comparision of σ and π bonds:
| σ bond | π bond |
| a) AOS overlap along the nuclear axis (line joining the nuclei), It is called linear combination of atomic orbitals (LCAO). | a) AOs overlap laterally ie. above and below the line joining the nuclear axis (side way overlap). |
| b) It is maximum overlapping and hence it is strong bond. | b) It is minimum overlapping and hence it is a weak bond. |
| c) Electron density is symmetrical around the nuclear axis. | c) Electron density is not symmetrical around the nuclear axis. |
| d) One lobes of each atom takes part in bond formation. | d) Two lobes of each atom take part in bond formation. |
| e) Any type of orbitals can involve in ‘σ ’ bond formation. | e) Only ‘p’ or ‘d’ – orbitals can involve in ‘π’ bond formation. |
| f) ‘ σ ‘ electrons are localized. | f) ‘π’ electrons are mobile electrons. |
| g) Shape of molecule is determined by ‘σ’ bonds formed by the central atom. | g) ‘π’ electrons do not determine the shape. |
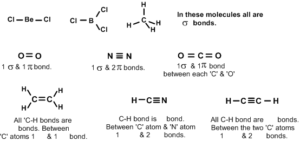
Double bond between two atoms represents 1’σ’ bond & 1’π’ bond. Triple bond represents 1’σ’ bond & 2 ‘π’ bonds.
Number of bonds between two atoms is called bond order. As bond order increases reactivity increase.
Atomic orbitals are represented with the help of wave functions, so orbitals have phase signs. A positive sign means a positive displacement of the wave (“up”) and a negative sign means a negative displacement (“down”). For‘s’ orbital generally shown positive sign.
When orbitals of two atoms come close to form a bond, their overlap may be positive, negative or zero depending upon the sign and direction of orientation. The following are possible and not possible orientations.
33. In between two atoms, if there is only one bond, it is bond’ σ ‘. If there are more than 1 bonds then one is ‘σ ‘and the other are ‘π ‘bonds.
34. Homonuclear molecules:
Eg: 1. H₂ molecule. H-H, 1 σ bond, s-s overlap. Both H atoms gain He configuration.
2. Cl2 molecule. C1-C1, 1σ bond, p-p linear overlap. Both C1 atoms gain Ar configuration.
3. P4 molecule.
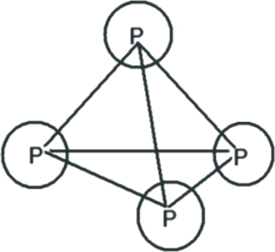
Each P atom makes 3 σ bonds. All are p-p linear overlaps.Shapes of P4 As 4 and Sb4 are equal.
Eg: 4. S8 molecule.
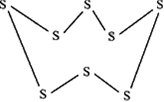
Each S atom makes 2 σ bonds. Both are p-p linear overlaps. It is called puckered ring structure. Puckered means non-planar.
35. Hetero nuclear molecules:
Eg:
1. H-Cl molecule.1 ‘σ’ bond. s-p overlap.
2. C1-F molecule 1’σ’ bond. p-p linear overlap.
Note: All diatomic molecules are linear.
36.
What is the reason to propose theory of hybridization?
Initially it was considered that unpaired electrons in the valence shell of an atom and only the pure atomic orbitals are involved in the bond formation, except when coordinate covalent bonds are formed This can explain the formation of molecules like H2, HX (where X = F, Cl, Br, I), X2, H2 O, NH3, etc However, the formation of BeH2, BH3 , and CH4 , (like compounds) cannot be explained, since Be has no unpaired electron in its ground state, and B and C also have 1 and 2 unpaired electrons respectively.
| Ground state electronic configuration | Excited state electronic configuration | Valency |
| Be : 1s22s22p0 | 1s22s12p1 | 2 |
| B : 1s22s22p12p02p0 | 1s22s12p12p12p0 | 3 |
| C : 1s22s22p12p12p0 | 1s22s12p12p12p1 | 4 |
The valence bond theory was modified to explain the formation of such compounds. It was suggested that in all such cases, a pair of electrons gets unpaired and one of the electrons is excited to the next available vacant orbital of slightly higher energy. The driving force for this process is the energy released in the bond formation by unpaired electrons. Accordingly, the number of unpaired electrons in Be, B, and C is 2,3, and 4 respectively.
Hence Be, B, C can show covalency of 2, 3 and 4 respectively. Apart from this, the existence of PF5 , SF6, IF7 , XeF2, XeF4 , XeF6 , can also be well explained by this theory.
If purely atomic orbitals were involved in bonding, then in the formation of methane molecule the three C-H bonds will be formed by the p-s overlap and the fourth C-H bond will be formed by the s-s overlap. Since the s-s overlap may take place from any direction. That means all the C-H bonds cannot be identical and all bond angles are not equal.
But in reality, this is not observed, instead we observe that
1. All HCH bond angles are identical with a value of 109°28′.
2. All C-H bond lengths and strengths are identical.
So to explain the above observations, the theory of hybridization was introduced.
To explain shapes and bond characters of molecules containing more than 2 atoms, the concept of Hybridisation is proposed. Bond length, Bond energy, and Bond angle are called Bond characters.
37. Intermixing of AOS of the same atom having nearly equal energy to form same No. of new identical, orbitals is called Hybridisation and the orbitals formed are called Hybridised orbitals.
38. Hybridised orbitals are as far away as possible so that there is minimum repulsion between them. That is why hybridised orbitals are more stable than unhybridised orbitals. They form stronger bond (σ) & never forms ‘π’ bonds.
39. Conditions of Hybridisation:
(a) AOs of the same atom can only take part.
(b) Participant AOS must have nearly equal or equal energy.
(c) All AOs having nearly equal or equal energy need not take part.
(d) Atom need not go to excited state in order to participate in Hybridisation.
(e) AOs having 2, 1 and no electron also can take part.
(f) Number of AOs participated and No. of hybridised orbitals formed must be same.
(g) Electronic arrangement must be same before and after hybridisation.
Note: Same atom can undergo different types of hybridisation under different situations.
More the directional bond greater is the bond strength
sp3 – sp3 > sp2 – sp2 > sp – sp > p – p > s – p > s – s
40. Different types of Hybridisation:
a) Sp Hybridisation: One s and 1 p orbital participate in hybridisation forming 2 equal sp hybridised orbitals which are linear. The angle between them is 180°. It is called linear or diagonal hybridisation. Each sp hybrid orbital possess 1/2s character & 1/2p character.
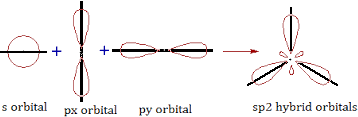
b) sp2 hybridisation: One ‘s’ and two ’p’ orbitals participate in hybridisation forming 3 equal sp2 hybridised orbitals which are planar. The angle between any two is 1200. It is called planar trigonal hybridisation. Each hybridised orbital possess ‘1/3’ ‘s’ character and ‘2/3’ ‘p’ character.
c). sp3hybridisation: One‘s’ and two’p’ orbitals participate in hybridisation forming 4 equal sp3 hybridised orbitals which are planar. The angle between any two is 109.280. It is called tetrahedral hybridisation. Each hybridised orbital possess ‘1/4’‘s’ character and ‘3/4’ ‘p’ character.
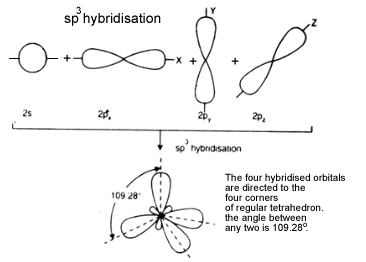
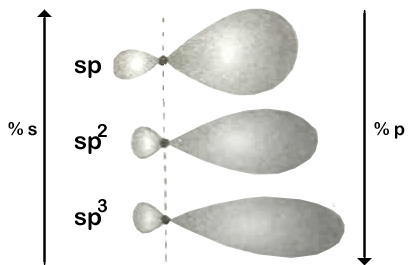
Shapes of hybrid orbitals with increasing ‘p’ character if shown in the above figure.
d) sp3 d hybridisation: One‘s’ and three ’p’ orbitals and one ‘d’ orbital participate in hybridisation forming 5 equal sp3 d hybridised orbitals. Three of them lie in the same plane which is planar and the angle between any two of them is 1200. The remaining two are perpendicular above and below the
plane. of the three hybridised orbitals which ate in the same plane. It is called trigonal bipyramidal hybridisation.
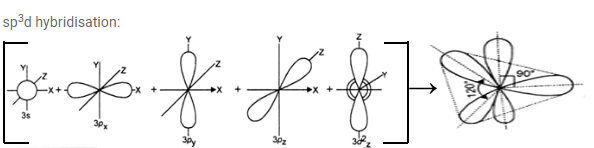Note: if ‘d’ orbital in valency shell participate, it is called outer orbital hybridisation and is denoted as sp3d. If‘d’ orbital in penultimate shell participates it is called inner orbital hybridisation and is denoted as dsp3. Inner orbital hybridisation is mainly seen in central atom of complex compounds.
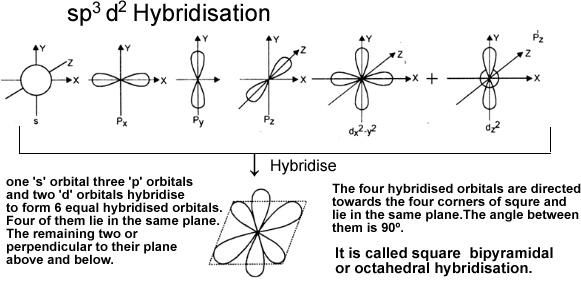e) sp3d2 hybridisation:
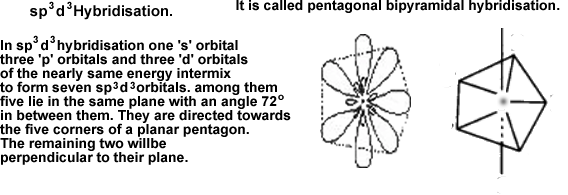
f) sp3d3 hybridisation:
g) dsp2:The orbitals involved in dsp2 hybridisation are dx2 – y2 ,s and two p-orbitals, geometry is square planar angle between any two dsp2 orbitals is 900. It is seen especially by transition metal ions.
[Ni(CN)4 ]-2 , [PtCl4 ]-2 etc
41. Calculation of steric number (SN):
For molecules/species having only one central atom the steric number of the molecule can be calculated as follows.
SN = [Q + (R/2)]. Where ‘Q’ is number of σ bond pairs and ‘R’ is number of unshared electrons on the central atom.
This will help to determine the shape of molecule.
For example in BeCl2, the central atom ‘Be’ has two σ bond pairs (Q=2) and has no unshared electrons. Then its SN value is [2 + (0/2)] = 2. It proves it has ‘sp’ hybridisation.
| Steric number | Hybridisation | Orientation of hybrid orbitals in space around the central atom | Angle between the hybrid orbitals. |
| 2 | sp | Linear | 1800 |
| 3 | sp2 | Trigonal planar | 1200 |
| 4 | sp3 | Tetrahedral | 109028” |
| 5 | sp3d | Trigonal bipyramidal | Axial(a) and equatorial(e) = 900.
e&e = 1200. a&a = 1800. |
| 6 | sp3d2 | Octahedral | Between two adjacent orbitals = 900.
Between two opposite orbitals = 900. |
| 7 | sp3d3 | Pentagonal bipyramidal | a&a =1800.
a&e = 900. e&e = 720. |
The following table will give a comprehensive view of hybridisation and examples of molecules or ions.
| Atomic orbitals participated | Hybridisation | Orientation of hybridised orbitals | Examples |
| one s + one p-orbital | sp | Linear | BeF2,BeCl2,C2H2 |
| one s + two p-orbitals | sp2 | Trigonal planar | BF3,C2 H4,NO3-1
CO3-2 |
| one s + three p-orbitals | sp3 | Tetrahedral | CH4 ,CCl4 ,SiF4 ,NH4+1 ,SO4-2 , ClO4-1 |
| one s + three p + d | sp3 d | Trigonal bipyramidal | PF5,PCl5 |
| one s + three p + two d | sp3 d2 | Octahedral | SF6 ,[CrF6 ]-3 ,IF5 |
| one s + three p+three d | sp3 d3 | Pentagonal Bipyramidal | IF7 |
| One d + one s + two p | dsp2 | Square planar | [Ni(CN)4 ]-2 , [PtCl4 ]-2 etc |
41. In a molecule we can know the hybridisation of the central atom with the following formula.
No.of Hybridised orbitals =
No.of bonds ’σ’ formed + No.of lone pairs remaining in the atom after all bonds are formed.
42. Shapes of molecules: This observation will help us to know the shapes of molecules.
No. of Electron pairs (EP) = No. of Bond Pairs (BP) + No. of Lone pairs (LP)
a) All diatomic molecules are Linear.
b) Triatomic molecules (AB2): No. of Electron pairs (EP) = 3.
i). Bent shape if the central atom has 1 or 2 loan pairs. Eg: H2O, H2S, SO2, SnCl2, PbC12 etc.
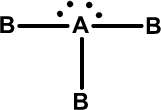
ii. Linear: if the central atom has 3 lone pairs (B-A-B) Eg: XeF2, KrF2, RnF2
iii) Linear if the central atom has no lone pairs. Becl2 Hgcl2 CO2, CS2 .
c) Tetra atomic molecule (AB3):
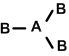
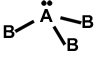
i. Planar trigonal shape: if the central atom has no LP. eg: BF3, BC13, AlCl3, S03 etc.
ii. Trigonal pyramidal shape in the central atom has 1 LP.
Eg: NH3, PH3, NF3, PC13, AsCl3, SbC13, etc.
iii. T-shape: If the central atom has 2LP.
Eg: C1F3, BrCl3, IC13 etc.
d) Penta-atomic (AB4)
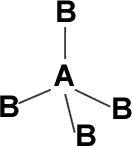
1. Regular tetrahedron shape: If the central atom has no LP and connected to identical atoms” Eg: CH4, CC14, Sic14, PbC14, SnC14 etc.
ii. Irregular tetrahedron: If the central atom has no LP and connected to different atoms.
Eg: CH3C1, CH2C12, CHC13, CHBI3, CHI3 etc.
iv. Square planar: If the central atom has 2 LP’s. Eg: XeF4 .
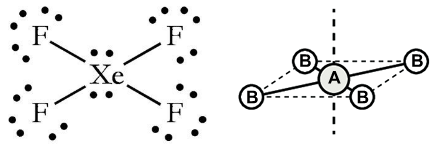
e) Hexa-atomic (AB5):
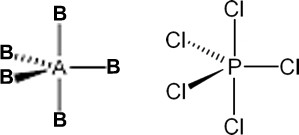
i. Trigonal Bipyramidal: If the central atom has no LP .
Eg: PC15, AsC15, SbC15 etc.
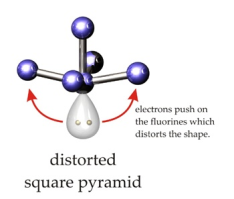
ii. Distorted square-pyramidal: If the central atom has 1 LP Eq: IF5, BrF5 etc.
f) Hepta-atomic molecule (AB6):
i) Octahedral or square bipyramidal if the central atom has no LP. eg: SF6.
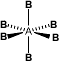
ii. Pentagonal pyramidal or distorted octahedral: If the central atom has 1 LP
Eg: XeF6
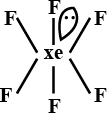
g) Octa-atomic molecule (AB7):
Pentagonal Bipyramidal. eg: IF7.
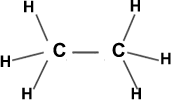
43. Shape of Ethane molecule (C2H6)
In Ethane each carbon atom is making 4σ bonds and no lone pairs. Each of them possesses sp3 hybridisation. All bong angle are 1090 .28’. No lone pairs on ‘C’ atoms.
Each carbon makes 3σ bonds with ‘H’ atoms. Total 6’C-H’ bonds.
The ‘C-C’ bond is ‘σ’ bond. Shape appears as two tetrahedrons fused at one corner. Molecule is non-polar (µ=0).
44. Shape of Ethylene or Ethene Molecule (C2H4): In Ethylene each Carbon atom possesses sp² hybridisation. That is why all bond angles are 120° and molecule is planar. . No lone pairs on ‘C’ atoms. Each carbon makes 2σ bonds with ‘H’ atoms. Total 4’C-H’bonds. In between carbon atoms there is one σ bond and one π bond. Molecule is non-polar (µ=0).
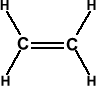
45. Shape of Acetylene or Ethyne molecule (C2H2):
In acetylene each carbon atom possess sp hybridisation because each of them is making 2σ bonds, one of them with ‘H’ atom and the second with other carbon. . No lone pairs on ‘C’ atoms.
In total there are 2 C-H ‘σ’ bonds and one C-C ‘σ’ bond. The remaining two bonds between carbon atoms ate ‘π’.
Molecule is linear and all bond angles are 180° because both Carbons possess sp bybridisation. It is nonpolar (µ=0).
46. Valency Shell electron pair repulsion theory (VSEPR):
a) The two primary founders of the VSEPR theory are Ronald Nyholm and Ronald Gillespie. This theory is also known as the Gillespie-Nyholm theory to honour these chemists. It explains the shapes of the molecules without taking hybridisation into consideration.
b) According to this theory in the central atom of a molecule the lone pairs or bond pairs must be arranged in such a manner so that there is minimum repulsion in between them. Pairs of electrons in the valence shell repel one another since their electron clouds are negatively charged. These pairs of electrons tend to occupy such positions in space that minimise repulsion and then maximise separation between them. A lone pair of electrons takes up more space around the central atom than a bond pair because the lone pair is attracted to one nucleus while bond pair is shared by two nuclei.
Repulsions of electron pairs around the central atom are LP-LP > LP-BP > BP-BP.
c) The double bond is in need of more space as compared to the single bond. The repulsion order in relation to the bonds is as follows: double bond – double bond > double bond – single bond > single bond – single bond.
d) . Keeping the central atom (having lone pair) same, if the electronegativity of the surrounding atom increases, the bond angle will decrease provided no other factors like size and back bonding play any role.
e) Keeping the surrounding atoms same, if the electronegativity of the central atom (having the lone
pair) increases, the bond angle increases.
f) Sometimes the lone pair may be transferred from filled shell of an atom to unfilled shell of the adjacent bonded atom. This phenomenon of transferring electron is known as ‘back bonding’.
g) If the central atom is surrounded by only bond pairs of electrons the molecule has a regular shape.
| Number of LPs | Number of BPs | Formula | Shape of molecule | Example |
| 2 | 0 | AB2 | Linear | BeCl2, BeF2, C2H2 |
| 3 | 0 | AB3 | Planar trigonal | BF3,BCl3 |
| 4 | 0 | AB4 | Tetrahedral | CH4,NH4+,CCl4 |
| 5 | 0 | AB5 | Trigonal bipyramidal | PCl5 |
| 6 | 0 | AB6 | Octahedral | SF6 |
h) In addition to bond pairs if the central atom has one or more lone pairs the molecule has irregular shape. Then the shape of the molecule can be visualized considering the various repulsions in the molecule. The shape with minimum repulsion is chosen.
Note: The location of lone pair/pairs will not be considered in the shape mentioned though they play important role to decide shape.
Let us see a simple calculation to know the minimum repulsions.
For example consider ClF3 molecule. The central atom ‘Cl’ will go to excited state [Ne]3s23p23p13p13d1. The three unpaired electrons of ‘Cl’ will be paired with the unpaired electrons of ‘F’.
Steric number is ‘5’.
Because Q= number of σ bonds = 3 and R = number of unshared electrons on the central atom = 4.
Steric number = [3 + (4/2)] = 5.
It has 2LPs and 3 BPs.
If the two LPs are at axial positions the possible repulsions in TBP arrangement are the following.
6 LP-BP repulsions.
If the two LPs are at equatorial positions the possible repulsions in TBP arrangement are the following.
4 LP-BP and 2 BP-BP repulsions.
Obviously second arrangement has less repulsion and then the shape is T-shape. The following table uses the same principle.
i) We will see another representation. Where A = central atom in the compound.
B = Atom connected to central atom and E=lone pairs on central atom.
| Number of BPs | Number of LPs | Formula | Shape of molecule | Example |
| 2 | 1 | AB2 E | Bent | SO2, O3 |
| 3 | 1 | AB3E | Trigonal pyramidal | NH3 |
| 2 | 2 | AB2E2 | Bent | H2O,H2S |
| 4 | 1 | AB4E | See saw | SF4 |
| 3 | 2 | AB3E2 | T shape | ClF3 |
| 5 | 1 | AB5E | Square pyramidal – distorted | BrF5 |
| 4 | 2 | AB4E2 | Square planar | XeF4 |
d) The various repulsions are as follows:
LP-LP > LP-BP > BP-BP repulsion.
e) The repulsion between 2 pairs is insignificant if the angle between them is 1200 or more than that.
Bent Rule: In a molecule the more electronegative atom prefers to stay in the orbital having less ’s’ character. Lone pair prefers to stay in the orbital having more‘s’ character.
For example in TBP geometry the more electronegative atom prefers to stay in the axial position and the lone pair prefers to stay in equatorial position.
How do we know the structure or shape of molecules?
These following some experimental methods used to know the shapes of molecules. (1). X-ray crystallography. (2).Mass spectrometry. (3). 13C NMR spectroscopy (4). 1H NMR spectroscopy. (5). Infrared spectroscopy. (6). Electron Paramagnetic Resonance (EPR or ESR – used for radicals mostly) etc.,
The findings based on the above are observed experimental facts.
Note: we must understand one important point here. In science observation is first and explanation is next. So every theory has its own limitations. Finally to explain the observed facts one has to use all theories in a judicial manner.
One such explanation making use of hybridisation and VSEPR theory is shown below to explain shapes of molecules.
| Hybridisation | Steric number | Possible values of [Q + (R/2)] | Shape | Examples |
| sp Hybridisation | 2 | 2+0 | Linear. | BeCl2,BeH2, BH2+1, NO2+1 etc. |
| 1+1 | Linear. | CO | ||
| sp2 | 3 | 3+0 | Trigonal planar. | BX3, AlCl3, AlBr3, CH3+1,CO3-2, NO3-1 etc. |
| 2+1 | Bent /Angular/ V-shaped. | NO2-1, SnCl2, SO2 etc. | ||
| sp3 | 4 | 4+0 | Tetrahedral. | BH4-1, NF4+1,NH4+1, SiF4, PH4+1 etc. |
| 3+1 | Pyramidal. | NH3, SnCl3-1, SO3-2, SeO3-2 etc. | ||
| 2+2 | Bent /Angular/ V-shaped. | H2O, Cl2O,NH2-1 etc. | ||
| sp3d | 5 | 5+0 | Trigonal bipyramidal. | PCl5, PF5, SbF5, PCl2F3, PCl2F3, XeO3F2 etc. |
| 4+1 | See –saw geometry. | SF4,SF2Cl2, XeO2F2 etc. | ||
| 3+2 | T – shape. | ClF3, XeF3+1, BrF3, XeOF2 etc. | ||
| 2+3 | Linear. | XeF2, ICl2-1, [I(CN)2]-1 etc. | ||
| sp3d2 | 6 | 6+0 | Octahedral. | TeCl6,SF6, XeO6-4, XeO2F4 etc. |
| 5+1 | Square pyramid. | IF5, XeF5+1, XeOF4 etc. | ||
| 4+2 | Square planar. | XeF4, [ICl4]-1 |
||
| sp3d3 | 7 | 7+0 | Pentagonal bipyramidal. | IF7 etc. |
| 6+1 | Distorted octahedral when the LP is in axial position. | XeF6, IF6-1, etc. | ||
| Perfect octahedral when the LP is in equatorial position. | [ICl6]-1, [TeCl6]-2, [SbCl6]-3 etc. | |||
| 5+2 | Pentagonal planar | [XeF5]-1 etc. |
Both hybridisation theory and VSEPR theory fails to explain the variation of bond angles and bond lengths in some molecules. There is considerable difference from their prediction. Let us see some examples.
In PH3.AsH3, and SbH3 the predicted bond angle must be slightly less than 109028”. Their experimental bond angles are 93.80,91.80 and 91.30 respectively.
In H2S, H2Se,H2Te the predicted bond angle must be slightly less than 109028”. Their experimental bond angles are 920, 910and 89.50 respectively.
Drago suggested an empirical rule to the above such variations.
According to him if the central atom belongs to 3rd period or below in the periodic table then the LPs will occupy a stereo chemically inactive ‘s’ orbital and bonding is mainly due to ‘p’ orbitals. Then the bond angle will be around 900.
In other words it means there is no hybridisation in such molecules.
47. Bond Characters:
a) Bond Length: It is the inter-nuclear distance between bonded atoms (where attractive forces are equal to repulsions). It is measured in A0 units. 1A0 =100pm. 1A0 = 0.0000000001 meters. 1pm(picometre) = 1×10−12 m.
Bond length is measured by spectroscopic, x-ray diffraction and electron –diffraction techniques.
In case of homo nuclear molecules sum of the covalent radius is bond length. It is because their electro negativity value is same and electron pair is shared equally.
It is not so in case of hetero nuclear molecules due the difference in electro negativity values. Then bond length is measured using Pauling’s empirical formula given below.
dAB = rA + rB + C(XA + XB) where ‘XA’ & ‘XB’ are the electronegative values of atoms A&B respectively. The value of C depends on the type of atoms involved in covalent bond.
For bonds involving atoms of 2nd period C = 0.08.
For bonds between Si, P and S bonded to more E.N atoms not belonging to first period C = 0.06.
If there are multiple bonds between atoms bond length decreases as bond order increases.
The ‘C-C bond length in 3HC-CH3 > 2HC=CH2 > HC≡CH. Their values are 1.54A0,1.33A0 &1.2A0 respectively. Another reason for this is ‘p’ character of hybrid orbital increases in the same order. For the same reason ion these compounds ‘C-H’ bond length also decreases. Their values are 1.09A0,1.08A0 and 1.06A0 respectively.
The bond length between a set of atoms in different molecules is always same.
eg: O-H bond length in H2O,H2O2 ,C2H5 OH is same i.e. 0.97A0.
If polarity of the bond is more, bond length is less. HF < HC1 < HBr < HI. Another reason for increase in bond length is size of bonded atom increases.
The shortest diatomic molecule is hydrogen. The bond length in H2 molecule is only 74 pm. The longest diatomic molecule is iodine. The bond length in I2 molecule is 267 pm.
b) Bond Enthalpy: (Bond dissociation energy) (Bond energy): It is the amount of energy required to break one mole of bonds of a particular type between two atoms in a gaseous state. It is measured in K Cals/ mole (Or) KJ/ mole.
It is the amount of energy released when one mole of bonds of a particular type are formed between two atoms in gaseous state.
If Polarity of the bond is more Bond energy is MORE.
If bond order is more BE is more. eg: In the compounds below see the values.
C-C bond energy in H3C-CH3 < H₂C = CH2 < HC≡ CH.
341 610 828 KJ/ mole.
As the number of lone pairs on a bonded atom increases, the bond enthalpy decreases. eg:
Even though the molecules contains similar bonds bond energy differs when one bond is broken since the nature of species differ. For example in water molecule (H2O) the energy needed to break the first O-H bond is 502KJ/mole. For the second the energy needed to break is 427KJ/mole. In such cases average is considered is used as bond enthalpy.
The magnitude of bond energy depends upon size of the bonded atoms.Bond energy in F2 is weak due to lone pair repulsions. Bond energy in H2 is strong because bond length is least. Bond energy in HF is strongest single bond because of high polarity. F2 < H2 < HF.
C) Bond angle: it is the angle between ‘σ’ bonds of the central atom in a molecule or complex ion. ‘π’ bonds are not considered.
It can be known with the help of Hybridisation and repulsion between LPs and BPs. As lone pair tries to occupy more space their presence on the central atom effects.
For example in water molecule ‘O’ atom has two lone pairs and possesses sp3 hybridisation but the bond angle is 1040 instead of 109.50. It is because the two lone pairs move apart pushing the bond pairs closer.
In ammonia molecule ‘N’ atom has one lone pair and possesses sp3 hybridisation but the bond angle is 1070 instead of 109.50. It is because the lone pair pushes the bond pairs closer. The less decrease in bond angle is because of one lone pair on the central atom.
Even the percentage of‘s’ character of the hybrid orbitals of the central atom is more bond angle is more. The actual reason is it changes the hybridisation of the atom. C – C bond angle C2H6 < C2H4 < C2H2 molecules.
In case of similar molecules of the same group as we go down the group size of the central atom increases and electro negativity decrease bond angle decreases. Example bond angle in NH3 > PH3 >SbH3 >BiH3.
If the central atom is same bond angle increases with the decrease in electro negativity of surrounding atoms NI3 > NBr3 > NCl3 > NF3.
Polarity and Dipole moment:
1. Whenever a covalent bone is established between atoms of different elements the electron pair will not be shared equally. The electron density increases on more electronegative. In other words the shared electron pair is slightly nearer to it. Therefore gore electronegative element gets a partial-ve charge (δ–) less electronegative element gets a partial +ve charge (δ+).
δ ≠ 0, δ ≠1 that means δ > 0 but δ <1. Magnitude of ‘δ’ is same.
This property of developing partial charges on bonded atom is called POLARITY. The bond is called polar covalent bond. Polarity of the bond can be considered as force acting towards more EN element.
2. In case of diatomic molecules, As E.N difference increases polarity of the molecule or bond increases. Eg: Polarity of HF > H-C1 > H-Br> H-1
3. Polarity of the molecule is referred with the name dipole moment (µ) and is measured in Debye units. It is named after the physicist Peter J. W. Debye.
1 Debye = 10-10 e.s.u.A0 or 10-18 e.s.u.cms.
1 Debye = 3.33564×10-30 C.m (S.I) where C= coulomb and m=meter.
For diatonic molecule µ = e × d. where ‘e’ is magnitude charge developed on bonded atoms and d= bond length.
4. In case of Polyatomic molecules polarity of the molecule (dipole moment) is the resultant of individual bond polarities or vector sum of the individual bond polarities.
5. Dipole moment of polyatomic molecule depends upon the following.
a) Geometry of the molecule
b) Strength of individual bond polarity.
NOTE: In a molecule bond will have polarity. Molecule may or may not have polarity.
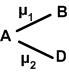
Calculation of resultant bond moment (dipole moment):
Let AB&AD are two polar bonds inclined at angle, their dipole moments are µ1 & µ2. The resultant dipole moment may be calculated using the following formula.
Dipole moment is helpful in predicting the geometry of the molecule.
Dipole moment can distinguish between symmetrical and non symmetrical molecules. Example both CO2 and H2O molecules are triatomic but former is n on polar and the later is polar. It is because water molecule is bent shape and the oxygen atom has two lone pairs.
Dipole moment of NH3 > NCl3 > NF3.
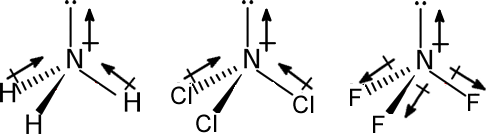
In NH3 the orbital dipole due to lone pair is in the same direction as the resultant dipole moment of the N – H bonds. The resultant is more ‘µ’ is more. In NCl3 molecule N-Cl bond polarity is less. That is why resultant is less ‘µ’ is less.
In NF3 molecule individual bond polarity is towards ‘F’ as ‘F’ is more electronegative than ‘N’. The resultant of individual bond polarities and that of lone is opposing. The net resultant value is less than ‘NH3’.
Dipole moment is useful distinguish cis and trans isomers. Cis isomer will have more dipole moment. You can see below the direction of resultants.
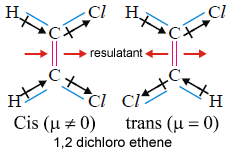
Dipole moment is greatest for ortho isomer, zero for Para isomer and less than that of Ortho or Meta isomer (Similarly substituted).
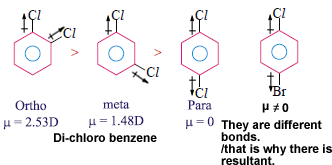
In these molecules ortho and meta isomers have dipole moment because individual bond polarities are acting in different directions. In case of Para isomer they act in exactly opposite direction so resultant is zero. In case of the fourth molecule though the individual polarities act in exactly opposite direction resultant is not zero as they are different atoms.
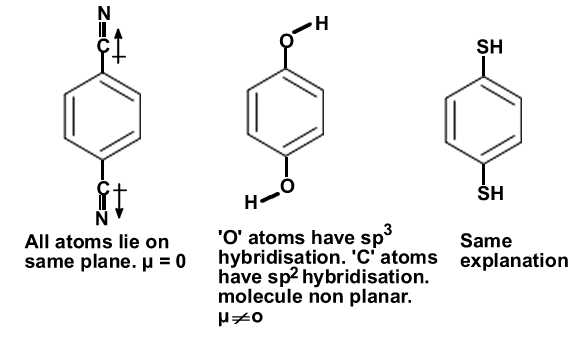
µ of CH3Cl >CH2Cl2>CHCl3. All are non planar.
Hybridisation of the central atom can be known with its dipole moment. eg:If the central atom in AB2 or AB3 type molecules has atomic number less than 21and ‘µ’ of the molecule is zero. Then the central atom will have sp hybridisation in AB2 and sp2 in AB3. Examples are BeF2 and BF3 molecules.
Dipole moment electro negativity difference eg: HF > HCl > HBr > HI.
If the number of lone pairs are more on the central atom dipole moment is more. HF > H2O >NH3. Reason LPs on F=3,O=2&N=1.
For homo atomic molecules and molecules having normal shapes such as linear, trigonal, tetrahedral posses zero dipole moment eg: Cl2 ,N2 ,O2 ,CO2.
Molecules having distorted shapes like angular,pyramidal shows dipole moment eg:H2O,SO2 e.t.c
Using dipole moment of the molecule – % ionic character of a covalent bond can be calculated as follows.
Hydrogen Bond: It is the weak electrostatic forces of attraction existing between partial positive charge present on H atom of one molecule and partial -ve charge present on more electronegative element of the adjacent molecule. Hydrogen bond is represented by a dotted line. It is also called protonic bridge. The distance between partial charges involved in H-bonding is more than the covalent bond length in that molecule. H – bonding is non directional.
Intra molecular H-bonding.
Hydrogen bond present in the same molecule is known as intra molecular hydrogen bond. It is a type of inter molecular attraction. Molecules which are bonded by H-Bonding are called associated molecules and liquid containing such molecules is called associated liquid. H-Bonding is non directional.
If H-bonding is present between molecules of different compounds it is called inter molecular H-bonding. It is called co-association. Compounds like NH3 Alcohol, HCOOH etc. are highly soluble in water due to co-association.
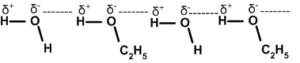
Inter molecular H-bonding. It is a best example for co- association.
Liquids which do not contain hydrogen bonds between their molecules are called normal liquids. Benzene, carbondisulphide, carbontetrachloride, acetone, ether, bromine, nitro benzene etc., are normal liquids.
Associated liquids have higher boiling points than normal liquids. The boiling point of an associated liquid depends on strength of hydrogen bond present in it and number of hydrogen bonds present in one mole of it.
eg: 1) The boiling point of water (1000C) is more than that of hydrofluoric acid (19.40C) though the hydrogen bond in HF is very strong. This is due to the presence of more number of hydrogen bonds in one mole of water than in one mole of HF.
eg: 2) The boiling point of water is more than that of ammonia though one mole of ammonia contains more hydrogen bonds than one mole of water. This is due to the presence of very strong hydrogen bonds in water than in ammonia.
H-Bonding is significant only in those molecules in which H is directly connected to 0. N or F. Chlorine atom very rarely involves in hydrogen bond.
Eg: HF, H₂O, NH3, C2 H5 OH, CH3 COOH, CH3OH, CH3NH2……
NOTE: H-Bonding stronger than Vander Waal’s forces of attraction.
The boiling points of NH3,H2O,HF are more than those of PH3 ,H2 S and HCl respectively because inter molecular hydrogen bonds are present in NH3 ,H2 O and HF. Hydrogen bonds are not present in the other three.
KHF2 exist but KHCl2 do not exist because HF2-1 ion there is intermolecular H-bonding.
Substances having intermolecular hydrogen bonds are highly water soluble. They have high boiling points and they are not steam volatile.
Some more examples of molecules having inter molecular hydrogen bond are o- Chlorophenol, o- Nitro phenol, o- Nitro aniline,o- Hydroxy benzaldehyde (Salicylaldehyde), o- Hydroxy benzoic acid ( Salicylic acid) e.t.c.
Some molecules like formic acid (HCOOH), acetic acid (CH3COOH) dimerise when dissolved in non polar solvents.
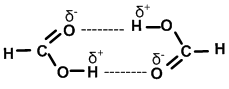
Due to dimerisation (because of H-bonding) their molecular weight will be twice the expected value when determined in non polar solvents.
Ice like solids, has a well-defined structure. Each water molecule is surrounded by four neighboring H2O molecules.The ice is a tetrahedral three dimensional polymer.
The two helical strands in the DNA molecule are joined by Hydrogen bonds.
Melting Point & Boiling point: M.P & B.P. depends upon inter molecular attraction. Inter-molecular attraction in covalent compounds are of two types (a) Vander Waals forces of attraction which depends upon size, mass and No. of electros. It increases as molecular weight increases.
(b) Hydrogen bonding:
NOTE: Among the given compounds the one having H-bonding which will have more MP and BP. H₂O, H₂S, H₂Se, H₂Te. Ans: (H₂O)
NOTE: If all the given compounds contain H-bonding, the one with more molecular weight will have more MP & BP. Among CH3OH, C2 H5 OH, C3 H7 OH, C4H9 OH. Ans: C4H9 OH.
NOTE: If none of the given compounds having H-bonding, the one with more molecular weight will have more MP & BP. Among CH4 ,C2H6 ,C3H8, ,C4H10. Ans: (C4H10).
Co-ordinate Covalent Bond (or) Dative Bond:
The bond formed between two atoms by the sharing of an electron pair which is contributed by only one of the two atoms is known as the co-ordinate covalent bond.
Co-ordinate covalent bond is also known as dative bond or semi polar bond or donor acceptor bond.
Co-ordinate covalent bond was proposed by Sidgewick. The name dative bond was proposed by Langmuir.
Co-ordinate covalent bond is represented by an arrow ( )the head of which is towards the atom which accepts the electron pair. Once formed is treated as covalent bond. Examples are: N2O, O3, N2O4, N2O5 CO, F3BNH3, B3N3H6, Al2Cl6 and in ions like H3O+, NH4+, NO3–,BF4–,e.t.c
In a hydrated cation the bond between water molecule and cation is dative bond. Every water molecule involves in one dative bond only.
eg: [Al (H2 O)6]+3 ion contains 6 dative bonds. [Be(H2O)4]+2 ion contains 4 dative bonds.
In complex molecule the bond between central metal atom and ligand is dative bond.
When octet is followed in order to obey it in central atom of some molecules like SO2,SO3,H2SO4 e.t.c. and in ions like SO4-2,PO4– dative bonds are used. This is modified now as octet rule is obsolete now. They are replaced by double bonds in modern concept.
In calculating covalency of an atom in a molecule or ion dative bond is treated as covalent bond. For example in hydronium ion covalency of O=3.
In sulphate ion covalency of S=6 etc.
Earlier to account for the octet of the central atom there is a practice of writing dative bonds in the
structures of SO2, SO3,Cl2O6 ,Cl2 O7 ,H2SO4, H3 PO4 ,
and in ions like SO4-2 ,PO4+3,ClO4-1 ,ClO3-1 ,ClO2-1 , SO3-2 etc.
Properties of Coordinate Covalent Compounds:
1. Those compounds having dative bonds will have more MP & BP than those of pure covalent compounds. They are also poor conductors like covalent compounds.
2. Readily soluble in non polar solvents.
3. Coordinate bond is represented by an arrow which means it is directed in specific orientation. That is why isomerism is observed in some of them.
Resonance: Occasionally no reasonable electronic picture can be drawn for a molecule which could satisfactorily account for its observed properties. For example, the electronic structure of carbon dioxide may be represented by at least three possible electronic arrangements given below.
(1) (2) (3)
The calculated heat of formation of carbon dioxide for formula (1) is 1464 kJ /mol and the 0-0 distance should be 2:40 A. However, the observed heat of formation is 1590 kJ/ mol and the O distance is 2.30A0. This indicates that none of these structures satisfactorily accounts for its observed properties. That means each structure explains some properties only but not all. Then the molecule is said to be in a state of resonance. The various imaginary structures are called resonating structures or canonical structures.
The real structure of the compound is known as resonance hybrid and that can explain all the properties. Our present knowledge about structures is not sufficient to represent resonance hybrid on the paper.
The word resonance for this situation should not give us an Impression that the molecule resonates from one structure to the other and the electron pair jumps back and forth from one bond to the other. This is totally wrong and the molecule has only one real electronic structure which cannot be physically described. Thus the difficulty lies in the description and not in the molecule itself.
Resonance is represented by double headed arrow. .
To represent the compound on the paper that resonating structure which explains most of the properties is used. It is considered to be most stable among the resonating structures.
The difference between the calculated heat of formation of the stable resonating structure and real heat of formation of the compound is called resonance energy. For any compound which is in state of resonance, the stability is more if resonance energy is more.
Chief conditions for resonance:
1. The arrangement of the atoms must be identical or almost so in every resonating structure.
2. The energy content of all the canonical forms must be nearly the same.
3. Each canonical form must have the same number of unpaired electrons.
Criteria of Resonance
The actual structure (Resonance hybrid) always will have less bond lengths compared to stable resonating structure.
The phenomenon of resonance is also noticed in many organic compounds. Thus benzene may be represented by the following.
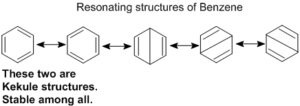
Kekule structures are used to represent benzene on paper.
Resonance energy of benzene is 150 kJ / mol, than the energy of kekule structures. This shows that the actual state is a hybrid intermediate between all these possible forms to that the ring is not formed by alternate double and single bonds but six equivalent bonds.
Some more examples are shown below.
The following are the general observations to decide more stable resonating structure because that is used to write on paper.
1. Uncharged resonating structures are more stable than charged.
2. Among the charged structures –ve charge on more electronegative element and positive charge on less electronegative element is more stable.
3. Among the charged structures those having minimum charge separation are more stable relatively.