Chemical equation is “Symbolic representation of a Chemical reaction”.
When one or more substances undergo chemical change to form one or more new substances the process is termed as chemical reaction. It is an observed fact. That means a process really occurring. A symbolic representation of such is called chemical equation.
Molecular Equation
See the following reaction in which the reactants are represented in their stable state of existence.
The arrow is read as ‘reacts to give’. The symbols on left of the arrow represent ‘reactants’ (starting materials). The symbol to the right of the arrow represents ‘products’ (final materials).
Zn + S → ZnS
In the above reaction ‘Zn’ and’S’ are reactants and ‘ZnS’ is the product.
Consider the action of dilute hydrochloric acid on granulated zinc to produce zinc chloride and hydrogen is represented in the following manner:-
Zn + HCl → ZnCl2 + H
Such an equation which simply represents the reactants and the products of a reaction by symbols and formulae of elements and compounds taking part therein is called a Skeleton equation. According to the law of conservation of matter (matter can neither be created nor destroyed by any physical or chemical change) the number of atoms of each element should be equal on both the sides. The equation which thus contains an equal number of atoms of each element on either side is called a balanced equation.
The balanced equation for the above reaction is as written as follows.
Zn + 2HCl → ZnCl2 + 2H
The above equation is yet an Atomic balanced equation. All constituents must be in molecular form hydrogen should be represented as H2, its molecule being di-atomic. The above equation then assumes the final form:
Zn + 2HCl → ZnCl2 + H₂
The balanced molecular equation, as above, is a true symbolic representation of a chemical reaction.
It is clearly evident in chemical reactions old bonds are broken (in reactants) and new bonds are formed (in products) resulting to the formation of products (new substances). The number of atoms of each element is remains same on both sides.
Among many types of chemical reactions the four important types of chemical reactions are the following.
1. Combination reaction.
One or more substances combine to form a product. 2Mg + O2 → 2MgO
2. Decomposition reaction.
A single substance changes to one or more products. CaCO3 → CaO + CO2
3. Displacement reaction. Zn + 2HCl → ZnCl2 + H2
4. Double Displacement reaction.
Two substances react to form two products by exchanging the components.
NaOH + HCl → NaCl + H2O
Chemical Equations:
Thevarious steps in writing an equation are:-
(1) Write the formulae or symbols of the reacting molecules on the left-hand side with a sign of (+) between them.
(2) In the same way write the formulae or symbols of the products (or resultants) on the right-hand side with the sign of (+) between them.
(3) The two sides are then combined with an arrow head (→ ) between them. This is then called a Skeleton equation.
(4) Multiply this equation by a suitable integer to make it a molecular equation.
It may be remembered that the molecules of all the elementary gases like hydrogen, oxygen, nitrogen, chlorine, bromine vapour, iodine vapour, etc., are diatomic, i.e., they consist of two atoms each and should be represented as such in complete equations.
Decomposition of lead nitrate on heating to produce lead oxide nitrogen peroxide and oxygen may be represented as below:-
(i) Pb(NO3)2 → PbO + NO₂+0…(Skeleton equation)
(ii) Pb(NO3)2 → PbO + 2NO2 + 0 (Balanced atomic)
(iii) 2Pb(NO3) → 2PbO + 4NO₂+ O2…(Balanced molecular)
Information conveyed by a Chemical Equation:
Like symbols and formulae, the, equations also have qualitative as well as quantitative significance.
(1) Qualitatively, the equation conveys the names of the reactants and products in the chemical reaction.
(2) Quantitatively it expresses the:
(i) Number of molecules of reactants and products taking part in the reaction,
(ii) Number of moles of each type of substance in the reaction.
(ii) weight-weight relationship or number of parts by weight of each type.
(iv) weight-volume relationship or relative weights and volumes of reactants and products. The gases evolved during the reaction.
The relation between molecular weight of a gas and its volume is that gram molecular weight of a gas occupies a volume of 22-4 liters at S.T.P. (Standard temp=0°c and pressure=760 mm Hg). This volume is known as gram molecular volume (G.M.V.).
Illustration:-
The above points can be illustrated by taking the following example:
CaCO3 + 2HCI → CaCl2 + CO2 + H₂O
The above equation tells us that:
(i) Qualitative relationship. Calcium carbonate reacts with hydrochloric acid to produce calcium chloride, carbon dioxide and water.
(ii) Quantitative relationship. One molecule of CaCO3 reacts with two molecules of HCI to produce one molecule of CaCl2, one molecule of CO2, and one molecule of water.
Or
One mole of CaCO3, reacts with 2 moles of HCl to produce one mole of CaCl2, one mole of CO2 and one mole of water.
Note. This is because each mole of a substance contains the same number of molecules, i.e., 6.023 x 1023 molecules.
(iii) Weight-weight relationship of reactants and products:
One molecule or [40+12+(3x 16)]=100 parts by weight of CaCO3 react with two molecules or [2x (35.5+1)]=73 parts by wt. of HCl to produce 1 molecule or [40+(2×35.5)]=111 parts by weight of CaCl2, 1 molecule or [12+(16×2)]=44parts by weight of CO2 and 1 molecule or [(1×2)+16]=18 parts by weight of water.
Total weight of reactants = 100 + 73 =173.
Total weight of products = 111 + 44 + 18 = 173.
(iv) Weight-volume relationship. 100 gm of CaCO3 react with 73 gm of HCI acid to produce 111 gm of CaCl2, 44 gm or 22-4 liters of CO₂ at S.T.P. and 18 gm of water.
Limitations or Shortcomings of a Chemical Equation and their Removal.
A chemical equation gives no information about:
(a) The conditions under which a reaction takes place. However the conditions may be indicated above the ‘arrow- head’ in term-‘Heated’, ‘Electrolysed’, ‘Solution’, ‘Catalyst’, etc.
Examples:
(i) Decomposition of potassium chlorate on heating to give potassium chloride and oxygen.
Heat
2KCIO3 → 2KCI + 30₂
(ii) Oxidation of sulphur dioxide in the presence of vanadium pentoxide, V2O5 (catalyst) at a temperature of 450°C
V2O5, 450°C
2SO2 + O2 → 2SO3
(iii) Combination of hydrogen and chlorine in the presence of sunlight to give hydrogen chloride.
Sunlight
H₂+ Cl₂ → 2 HCI
(b) The physical state of the reactants or the products, i.e., it does not tell us whether they are solids, liquids or gases. This can, however, be done by using the symbols (s), (1), (g) and (aq) for solid, liquid, gas and aqueous solution respectively. Thus the equation
Zn (s) + H₂SO4 (aq) →ZnSO4 (aq) + H2 (g) shows that solid zinc reacts with dilute sulphuric acid to produce zinc sulphate solution and hydrogen gas.
Further an arrow pointing upwards (↑) indicates that the product is a gas and escapes. An arrow pointing down indicates that the product is insoluble and settles down as a precipitate, e.g.,
FeS + H₂SO4 → FeSO4 + H2S↑
AgNO3 +NaCl → AgCl (precipitates) + NaNO3
(c) Heat changes involved. Ordinarily it does not tell whether heat is evolved or absorbed in the reaction. But heat changes can be indicated in the equation by showing the heat involved on the right hand side. If the reaction is exothermic, plus sign (+) is used and if it is endothermic, negative sign (-) is used.
C+ O2 → CO2 + 94 kcal. (Exothermic reaction)
It means when one mole of carbon burns in one mole of oxygen molecules to produce one mole of carbon dioxide, 94 kilogram calories of heat are set free.
C+2S → CS2-26 kcal.
Or
C+2S + 26 kcal → CS2(Endothermic reaction)
It means that 26 kilo calories of heat are absorbed when one mole of carbon disulphide is produced from its elements.
(d) Concentration of the reactants or the products is not known.
In case of reactants, this may be indicated by putting the word conc. for concentrated and dil. for dilute before the formulae of the reactants, e.g.,
Heat
Cu + Conc, 2H,SO4 → CuSO4 + SO₂+ 2H₂O
Mg+dil. 2HCl → MgCl2 + H₂
(e) Time taken by the reaction to complete itself.
(f) The rate at which the reaction takes place, i.e., whether it takes place slowly or quickly.
Balancing of a Chemical Equation:
Before balancing a chemical equation, the student should ensure that all the substances taking part in the reaction, i.e., both reactants and the products have been represented by their correct formulae. During balancing, only the relative number of the molecules of different substances can be changed and not their formulae as these are fixed by valency considerations. Two methods are generally usedfor the balancing of an equation, i.e., equalization of atoms of element on either side of the equation.
(a) Hit and trial method. This method is usually successful in the case of simple equations, in which no element occurs in more than one compound on either side, e.g.,
Zn+ H₂SO4 → ZnSO4 + H₂
(b) Partial equations method. This method is tried in such cases where hit and trial method fails, i.e., in complex equations in which one or more elements occur in more than one compound on either side, e.g.,
3Cu + 8HNO3(Dilute) → 3Cu(NO3)2 + 2NO + 4H₂O
In this reaction have two steps.
Copper nitrate is formed by the reaction of copper and dilute HNO3 and hydrogen.
Hydrogen produced reacts with HNO3 to form NO and H2O.
[Cu + 2HNO3 → Cu(NO3)2 + 2H] x 3
2HNO3 + 6H → 2NO + 4H2O
(c) Oxidation number method.
(d) Ion electron (Half-reaction) method.
(A) Hit and trial method. For this purpose, the compound with the largest number of atoms is selected first of all and its constituent atoms are equalized on the opposite side, by increasing the number of molecules of the compounds containing those elements. The process is repeated with the molecules of the other compounds on the right hand-side and the left-hand side till the number of atoms of all elements involved is equalized on both sides. The following points are valuable in trying hit and trial method.
(a) A compound with the biggest formula is selected to make a start.
(b) If the above step fails, the element which occurs in minimum number of compounds on either side is first chosen and is equalized on both sides. The one which occurs in the largest number of compounds is selected and equalized last of all, while others in between are selected one after the other in turn.
(c) Whenever elementary gases like hydrogen, chlorine, oxygen, etc., are involved in an equation, these are represented in their atomic form first and later on the entire equation is made molecular by multiplying with two.
The following example will make the method clear.
Iron reacts with steam to produce the magnetic oxide of iron and hydrogen. The skeleton equation for the reaction is:-
Fe+H2O ⇋ Fe3O4+ H
Selecting the compound Fe3O4 which has largest number of atoms, 3 atoms of Fe on the R.H. side can be equalized in the LH side by taking 3 atoms of Fe into account. Again, 4 atoms of O in side can be equalized on the L.H. 4 molecules of steam. Thus O and Fe are balanced on both the sides of equation. In 4 molecules of steam on the L.H. side, there are 8 atoms of H, therefore, on the R.H. side also there should be 8 atoms of H. Thus, the balanced atomic equation will be:
3Fe+ 4H2O ⇋ Fe3O4+ 8H
In order to make the equation molecular, the number of H atoms may be halved to represent them as 4 molecules, every other substance being already in its molecular form.
3Fe+4H₂O ⇋ Fe3O4+ +4H₂
(B) Partial equations method. The hit and trial method is very tedious and lengthy in certain cases. Besides, in many cases, it does not succeed and the partial equations method is used instead. The method may be summarised as mentioned below:
(i) The bigger molecules are split up into a number of simpler ones or the whole reaction is supposed to proceed in a number of steps or stages.
(ii) Simple balanced equations are written for the reaction of each of the simple components of bigger molecules or separate balanced equations are written for the individual steps or stages.
(iii) The step equations or partial equations are finally added in such a way that the intermediate products (Not appearing in the final products) cancel one another.
(iv) The equation is suitably converted to make it molecular.
The following example will illustrate the method.
(a) Skeleton equation:
KMnO4 + H2SO4 → K2SO4 + MnSO4 + H2 O+ [0]
This reaction is supposed to proceed in the following steps:
(i) KMnO4 is supposed to be split into K2O, MnO, (inter- mediate products) and oxygen.
(ii) K2O and MnO react with sulphuric acid separately to form the corresponding sulphates and water.
(iii) Excess of oxygen is evolved as such. Representing these reactions by balanced partial equations we have:
2KMnO4 → K2O + 2MnO + 5[0] ———(i)
K2O + H2SO4 → K₂SO4 + H₂O ——–(ii)
MnO+ H2SO4, → MnSO4 + H₂O ——-(iii)
Multiplying the equation (iii) by 2
2MnO+2 H2SO4 → 2MnSO4 +2 H₂O
And then adding (i), (ii) and (iii), to cancel out MnO we get-
2KMnO4 + 3H₂SO4 → K2SO4 + 2MnSO4 +3H2O+5[0]
The equation is now made molecular by multiplying the whole equation by 2, and we have the equation:
4KMnO4 + 6H₂SO4 → 2K2SO4 + 4MnSO4 +6H2O+5O2
Types of Reactions
Chemical reactions can be broadly divided into two types.
(1) Reactions in which no electron transfer takes place, i.e., reactions in which just joining or separating of ions or molecules involves no electron transfer. Simple precipitation ionic reactions, acid-base neutralization reactions, direct decomposition of covalent molecules come under this type.
(2) Reactions in which there is electron transfer from one atom to another. These are known as oxidation-reduction reactions.
Precipitation Ionic Reactions
When silver nitrate solution is added to sodium chloride solution, a white precipitate of silver chloride is formed. In aqueous solution, both the salts are present in the form of ions.
Ag+ (aq) + NO3-1 (aq) + Na+ (aq) + Cl-1(aq) →Ag Cl (s) + Na+ (aq) + NO-1 (aq)
The Ag+ and Cl-1ions join together in large aggregates of AgCl which being insoluble in water is precipitated. Na+ and NO3-1, remain just as they were initially. Thus a precipitation ionic reaction is termed as the grouping ofoppositely charged ions to form large aggregates of an insoluble ionic compound which separates out as solid.
As Na+ and NO3-1ions have not undergone any change, they can be cancelled out in writing the equation of the net reaction.
Ag+ (aq) + Cl-1 (aq) → Ag Cl (s)
The ions which do not undergo any change in an ionic reactionare sometimes called spectator ions. (In the above reaction, Na+and NO3-1 are spectator ions.
In the chemical calculations the weights of the substances are required and hence total equation is written, as-
AgNO3 + NaCl → AgCl + NaNO3
When barium chloride solution is added to potassium sulphatesolution,
Ba²+ (aq) + 2 Cl-1(aq) + 2K+ (aq) + SO42- (aq) → BaSO4 (s) + 2K+ (aq) + 2C1– (aq)
The net equation is
Ba²+ (aq) + SO42- (aq) → BaSO4 (s) ↓
For calculations the equation is
BaCl2 + K₂S4→ BaSO4 + 2KCI
Acid-Base Reactions
According to Arrhenius theory of acids and bases, a substancewhich gives hydrogen ions (H+) in an aqueous solution is an acid and the substance that gives hydroxyl (OH-1 ) ions is base.
Aq
HA → H+ + A–
Acid
Actually H+ ions will be in the form of hydronium (H3 O+) ions in aqueous solution.
Aq
MOH → M+ + O–H the negative charge is on oxygen atom as it has one electron extra.
Base
Strong acid and strong base completely dissociate into ions.
Examples.
HCl,H2SO4,HNO3…are strong acids.NaOH,KOH …are strong bases.
CH3COOH,H3PO4 ….. Are weak acids. NH4OH,Ca(OH)2 …. are weak bases.
Note: Lowry-Bronsted theory and Lewis theory explain the properties of acids and bases in a better way. But Arrhenius theory is sufficient for chemical calculations; hence the acid-base neutralisation reactions are explained mainly by Arrhenius theory in this lesson.
Acid -base neutralization reactions:
According to Arrhenius theory nuetralisation means the H+ ions furnished by acid in aqueous solution combine with the O–H ions furnished by base in aqueous solution to water molecules.
Example : HCl + NaOH → NaCl + H2O.
If acid, base or both are weak complete ionisation does not occur and the unionised weaker component remains in molecular state and will be represented as such in equation.
Example: HCl +NH4OH →NH4+ + H2O
But the equation for calculations is HCl + NH4OH → NH4Cl + H2O
Oxidation – Reduction or Redox reactions.
Now we go to the second category of chemical reactions which involve transfer of electrons.
After understanding the concept of oxidation and reduction thoroughly we will learn the balancing of such reactions.
Loss of electrons is oxidation and gain of electrons is reduction.
Let us see the formation of NaCl from Na and Cl2.
2Na + Cl2 →2NaCl……balanced equation.
The process takes as follows.
2Na −2e– → 2Na+ that means each sodium ion loses an electron to form unipositive ion (Na+).
2Cl + 2e– → 2Cl– that means each chlorine atom gains an electron and changes to uninegative ion (Cl–).
Here Na is oxidized to Na+ and Cl is reduced to Cl–.
Note: An atom can lose electron provided there is another atom or atoms which takes it. That means oxidation and reduction go hand in hand.
The atom that takes electron is called oxidising agent and the atom which loses electron is called reducing agent.
In the above example ‘Cl’ is oxidising agent and ‘Na’ is reducing agent.
This theory is very useful in case of simple atoms or ions. But in case of polyatomic molecules or ions it is difficult to apply. To understand such we must use oxidation number method.
Oxidation number is the charge represented on the top of the element which the element appears to possess.
Example 1:
NaCl it is an ionic compound and the charges on the elements Na & Cl is +1 & -1 respectively. Here sodium really lost an electron and ‘+1’ charge is really present so its charge is its oxidation number. Similarly chlorine gained an electron and ‘-1’ charge is really present so its charge is its oxidation number.
Example 2:
CaO is an ionic compound and the charges on the elements ‘Ca’ and ‘O’ are +2 & -2 respectively. Here calcium really lost 2 electrons and ‘+2’ charge is really present so its charge is its oxidation number. Similarly oxygen gained 2 electrons and ‘-2’ charge is really present so its charge is its oxidation number.
Example3:
Consider HCl molecule ( H∙∙Cl). They are sharing an electron pair to form a covalent bond but the sharing is not identical as ‘Cl” is more electronegative than ’H’. The shared electron pair will be nearer to chlorine. So ‘H’ atom in this molecule is considered to be having ‘+1’ oxidation state and ‘Cl’ atom in this molecule is considered to be having ‘-1’ oxidation state. Remember that charges are not present on the atoms but oxidation numbers are ‘+1’ and ‘-1’.
Example4:
Consider CO2 molecule (O :: C :: O). carbon atom has four electrons in its valance shell and oxygen has six electrons in its valance shell. So carbon atom in these molecule shares two electrons from each oxygen atom and each oxygen atom shares two electrons from carbon atom.
Remember oxygen atom is more electronegative than carbon atom so the shared electrons pairs will be nearer to oxygen atom compared to carbon atom. So oxidation number of each oxygen atom in this molecule is ‘-2’.
In total four electrons of carbon are shared more by oxygen. So oxidation number of carbon atom in this molecule is ‘+4’.
Note: sum of the oxidation numbers of elements in a molecule must be zero as molecules are neutral.
Example5:
Consider SO42- (sulphate Ion). Its structure is as follows.
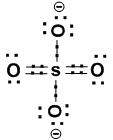
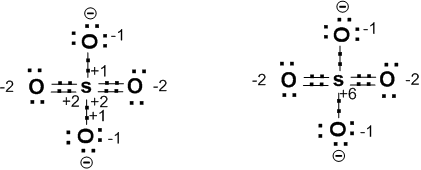
In this ion ‘S’ atom is sharing ‘2’electrons from ‘2’oxygen atoms and ‘1’electron from ‘2’ oxygen atoms. We know ‘O’ atom is more electronegative than ‘S’ atom. So the shared electrons will be nearer to ‘O’ atoms and the ‘S’ atom will have an oxidation number ‘+6’. The two’O’ atoms sharing ‘2’ electrons will have oxidation number ‘-2’. The two ‘O–‘will have oxidation number ‘-1’ respectively.It can be represented as shown above.
Example6: PO4-3 (phosphate ion) .its structure is as follows.

In this ion ‘P’ atom is sharing ‘2’electrons from ‘1’oxygen atom and ‘1’electron from ‘3’ oxygen atoms. We know ‘O’ atom is more electronegative than ‘P’ atom. So the shared electrons will be nearer to ‘O’ atoms and the ‘P’ atom will have an oxidation number ‘+5’. The ’O’ atoms sharing ‘2’ electrons will have oxidation number ‘-2’. The three ‘O– ‘will have oxidation number ‘-1’ respectively. It can be representedas shown below.

Like this electronic structure can be drawn for each molecule and ion and oxidation number of each atom can be known but the process is very laborious.
Hence the following operational rules are derived for convenience from the study of structures.
Note: The oxidation state of an element may be +ve,–ve , zero or fractional value.
1. Oxidation number is zero for the following.
For all elements whose atoms have individual existence at STP.
Oxidation number of Na,Ca,K ……oxidation number is zero in uncombined state.
Oxidation number of elements which exist as molecules the oxidation number is zero.
H2,O2,F2, Cl2,P4,S8 …. oxidation number of the respective elements is zero.
Oxidation number is zero for all inert elements in uncombined state.
Oxidation number is zero for carbon in diamond and graphite.
Oxidation number is zero for any element in its allotropic form.
2. Oxidation number of the mono atomic ion is equal to the charge.
Oxidation number of ‘Na’ in Na+1 =+1, ‘Ca’ in Ca2+ = +2,’Al’ in Al+3 = +3……….
Oxidation number of ‘Cl’ in Cl-1 = -1, ‘O’ in O-2 = -2, ‘N’ in N3- = -3 …….
3. The oxidation number of ‘F’ in all compounds containing ‘F’ is -1 as it is highly electronegative.
4. The oxidation number of ‘H’ is +1 when it is connected to more electronegative element than it.
In compounds HCl,H2O,NH3 ……..
The oxidation number of ‘H’ is -1 in all hydrides. Example NaH,CaH2……..
5. The oxidation number of ‘O’ is -2 in all oxides.
-1 in peroxides (Na2O2,H2O2..).
-(1/2) in super oxides (NaO2,KO2..).
+2 in F2O and +1 in F2O2.
6. Oxidation state of alkali metals and alkaline earth metals in its compounds is +1, +2 respectively.
7. Highest oxidation number possible is +8 e.g.: oxidation number of Ru in RuO4, Os in OsO4
and Xe in XeO4.
8. For a neutral molecule, the sum of the oxidation numbers of all the atoms in it is equal to zero.
Example: Let us take K2S O4 = [2x(+1)]+[1x(+6)]+[4x(-2)] = 2+6-8=0.
9. For a polyatomic ion, the algebraic sum of the oxidation numbers of all the atoms is equal to the charge on it.
E.g.: consider NO3-1 ion.
Oxidation number of N=+5, for three oxygen atoms oxidation number = (-2×3) = -6.
+5-6=-1(charge on the ion).
10. For a covalent compound the oxidation state of an atom is equal to the number of covalent bonds in which the atom involves but the sign (+ or -) depends on the connecting atoms.
Example:Phosgene molecule COCl2.
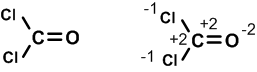
oxidation state of O = (-2); Cl =(-1) and C = (+4).
Example: let us consider CHCl3 molecule.
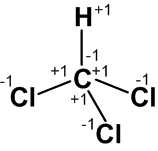
Carbon atom is making four covalent bonds (3 with chlorine atoms and one with hydrogen atom). Chlorine is more electronegative than carbon, so the oxidation number of each chlorine atomis (-1) and each of the carbon atoms will have oxidation number of ‘+1’. As carbon is connected to more electronegative chorine its electronegativity will be more than hydrogen as a result the oxidation number of ‘H’ is ‘+1’and that of carbon is ‘-1’. See the following geometry of molecule with oxidation states represented.
In this molecule the net oxidation state of carbon = [3x(+1)] -1 =+2.
11. The maximum oxidation state of an element should never exceed its group number.
12. The oxidation state of a metal in metal carbonyls is zero
e.g.: Ni (CO)4 ; Fe (CO)5 ; Cr (CO)6.
13. Oxidation state of metal in amalgam is zero.
14. Fractional oxidation state is the average oxidation state of the element under examination.
For example consider C3O2 molecule.
Oxidation number of ‘2’ oxygen atoms = (-2×3) =-4.
Oxidation numbers of ‘3’ carbon atoms must be ‘+4’.
For one carbon oxidation number is (+4/3).
In reality it is not so. The structure of above molecule is as follows. It is shown with the actual oxidation numbers of elements.
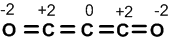
Out of the three ‘C’ atoms two have oxidation number (+2) while the third carbon has zero oxidation number in the compound.
Using the above rules let us calculate the oxidation numbers of certain elements in their compounds.
(a). Oxidation number of ‘Cr’ in K2CrO4.
We know oxidation numbers of K =+1 and O = -2. Let us use them assuming oxidation number of ‘Cr’ = z.
K2CrO4 =[2 x (+1)] + (1xz) +[ (4 x( -2)] = (+2) + z +(-8) = z – 6.
We know molecules are neutral. So z-6 = 0 and z = 6.
(b). oxidation number of ‘Mn’ in KMnO4.
We know oxidation numbers of K =+1 and O = -2.
Let us use them assuming oxidation number of ‘Mn’ = z.
KMnO4 = [1 x (+1)] + (1 x z) +[4x(-2)] = z-7.
We know molecules are neutral. So z-7 = 0 and z = 7.
(c) . Oxidation number of ‘Cr’ in [Cr2O7]-2 ion.
We know the oxidation number of ‘O’ is ‘-2’. Let us assume the oxidation number of ‘Cr’ = z.
[Cr2O7]-2 = [2xz] + [7 x (-2)] = 2z – 14.
The sum of the oxidation numbers of elements in a polyatomic ion must be equal to the charge of the ion. That is (2z – 14) = -2.
2z= -2+ 14 = 12 and z= (12/2) =6.
According to oxidation number concept oxidation means increase in oxidation number and reduction means decrease in oxidation number.
Let us consider the following reaction.
2Mg + O2 → 2MgO.
Oxidation number of atoms in elementary state is zero.
In MgO oxidation number of ‘O’ is ‘-2’ so obviously the oxidation number of ‘Mg’ is ‘+2’.
That means in this reaction oxidation number of ‘Mg’ increase from ‘0 to +2’. That is it is oxidised, the oxidation number of ‘O’ decreased from’ 0 to -2’. That is it is reduced.
That means in this reaction ‘Mg’ is reducing agent and ‘O2’ is oxidising agent.
Conversion of ‘Fe+2 to Fe+3‘,‘Sn+2 to Sn+4’ are examples of oxidation.
Conversion of ‘Cl2’ to ‘2Cl-1’, ‘O2 to 2O-2’ are examples of reduction.
This concept can be well understood by practicing with more examples.
Balancing chemicalequations by oxidation number method.
The principle in this method is conservation of charge. That means the number of electrons lost during oxidation must be equal to the number of electrons gained during reduction. To say in other words the increase in oxidation number and decrease in oxidation number must be same.
Consider the following equation.
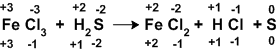
Actual oxidation numbers of elements is represented at the bottom. Depending upon the number of atoms total value is represented on the top to show molecule’s neutral nature.
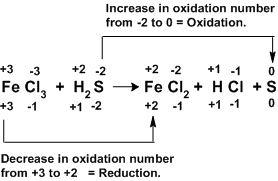
The above reaction indicates that each ‘Fe+3’ gained and electron and each ‘S-2’ lost two electrons. To balance the loss and gain of electrons two iron atoms are required for each sulphur atom.
It means there must be two ‘FeCl3’ molecules for each ‘H2S’ molecule in reactants.
2FeCl3 + H2S →FeCl2 + HCl + S
Now we have to balance on the product side. It can be done by interchanging their coefficients as shown below.
2FeCl3 + H2S → 2FeCl2 +2 HCl + S
Let us summarise what the procedure is adopted above.
1. Write the oxidation number of each element on the top of the symbol then determine which is oxidised and which is reduced. Usually only two elements change one gains and other loses.
2. Balance the gain and loss in oxidation numbers. It can be done by placing the change in oxidation number of reducing agent in front of the formula of oxidising agentand vice versa in reactant side.
3. Complete the balancing of elements which have changed the oxidation numbers on the right hand side (products side). Then balance the other atoms.
Let us see some more examples for better understanding.
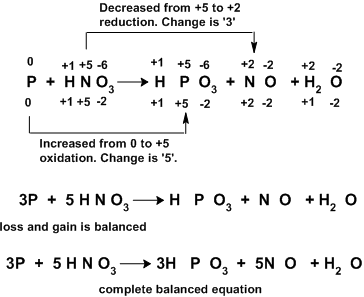
Balancing ionic oxidationreduction equations.
If we omit the ions which are not taking part in the reaction, it is said to be in ionic form.
Example 1:
Consider the following reaction.
Cu + HNO3 → Cu(NO3)2 + NO + H2O
In this reaction ‘Cu’ is changing to ‘Cu+2’ ion, that means copper is oxidised and its oxidation number increased from ‘0 to +2’. At the same time ‘N’ in (NO3)-1is reduced and its oxidation number decreased from ‘+5 to +2’.
Cu is reducing agent and (NO3)-1 is oxidising agent.
Let us write ionic equation for the above.
Cu + H+ + (NO3)-1→ Cu+2 + NO3– + NO + H2O
What we understand from the above equation is only some of the (NO3)-1ionhas undergone the change. Now we will rewrite the equation as follows omitting (NO3)-1 on the product side.
Cu + H+ + (NO3)-1→ Cu+2 + NO + H2O
Now we will rewrite by placing the change in oxidation number of reducing agent in front of the formula of oxidising agent and vice versa in reactant side and balance on the product side.
3Cu + 8H+ + 2(NO3)-1 → 3Cu+2 + 2NO + 4H2O
Now we will add unreacted (NO3)-1 on both sides to complete balancing.
3Cu + 8H+ + 2(NO3)-1 + 4(NO3)-1 → 3Cu+2 + 2NO + 4(NO3)-1 + 4H2O.
Example 2:
Consider the following reaction.
KMnO4 + H2SO4 + H2S → K2SO4 + MnSO4 + S + H2O
In this reaction ‘(MnO4)-1’ is changing to ‘Mn+2’ ion, that means ‘Mn’ is reduced and its oxidation number decreased from ‘+7 to +2’, at the same time ‘S’ in ‘H2S’ is oxidised and its oxidation number increased from ‘-2 to 0’.
‘(MnO4)-1’ is oxidising agent and ‘H2S’ is reducing agent.
Let us write ionic equation for the above.
MnO4– + H++ H2S → Mn+2 + S + H2O
We have omitted the ‘(SO4)-2’ and ‘K+’ ions as they have not undergone any change.
Now we will rewrite by placing the change in oxidation number of reducing agent in front of the formula of oxidising agent and vice versa in reactant side and balance on the product side.
2MnO4– + H+ + 5H2S → 2 Mn+2 + 5S + H2O
Balance oxygen and hydrogen atoms.
2MnO4– +6 H+ + 5H2S → 2 Mn+2 + 5S + 8H2O
Now we will add unreacted ions ‘(SO4)-2’ and ‘K+’ on both sides.
2K+ + 2MnO4– +6 H+ +3SO4-2 + 5H2S →2K+ + 2 Mn+2 + 3SO4-2 + 5S + 8H2O
Example 3:
Consider the following reaction.
K2Cr2O7 + FeSO4 + H2SO4 → Cr2(SO4)3 + Fe2(SO4)3 + K2SO4 + H2O
In this reaction ‘(Cr2O7)-2’ is changing into ‘Cr+3’that means ‘Cr’ is reduced and its oxidation number decreased from ‘+6 to +3’, at the same time ‘Fe+2’ is oxidised and its oxidation number increased from ‘ +2 to +3’.
‘(Cr2O7)-2’ is oxidising agent and ‘Fe+2’ is reducing agent.
Let us write ionic equation for the above.
Cr2O7-2 + Fe+2 → Cr+3 + Fe+3
We have omitted the ‘(SO4)-2’ and ‘K+’ ions as they have not undergone any change.
Now we will rewrite by placing the change in oxidation number of reducing agent in front of the formula of oxidising agent and vice versa in reactant side and balance on the product side.
Cr2O7-2 + 6Fe+2 → 2Cr+3 + 6Fe+3
Balance oxygen and hydrogen atoms.
Cr2O7-2 + 6Fe+2 + 14H+ → 2Cr+3 + 6Fe+3 + 7H2O
Now we will add unreacted ions ‘(SO4)-2’ and ‘K+’ on both sides.
2K+ + Cr2O7-2 + 6Fe+2 + 6SO4-2 +14H+ + 3SO4-2
→ 2K+ +SO4-2 +2Cr+3 +3SO4-2 +6Fe+3 +9SO4-2 + 7H2O
Or
2K+ + Cr2O7-2 + 6Fe+2 + 14H+ +13SO42- →2K+ + 2Cr+3 + 6Fe+3 +13SO42- + 7H2O
Balancing of chemical equations by Ion-electron method or Half reaction method:
This is a convenient method to balance ionic equations. Most of the reactions in solution are ionic. This method is adopted using the following steps.
1. Identify the ions which have undergone oxidation and reduction and write them as two separate reactions. They are called oxidation half reaction and reduction half reaction.
2. Balance all atoms other than ‘H’ and ‘O’ in both half reactions.
3. To balance oxygen atoms add ‘H2O’ molecules to the side deficient in ‘O’ atoms.
4. In acid solution add ‘H+’ to the side deficient in ‘H’ atoms in the same number.
5. In basic solution add one ‘H2O’ for each ‘H’ to the side having less ‘H’ atoms. At the same time add same number of ‘(OH)-1’ions on the other side.
6. Add electrons to products in oxidation half reaction to balance the charge.
7. Add electrons to reactants in reduction half reaction to balance the charge.
8. Multiply one or both half reactions so that the loss of electrons and gain of electrons are same.
9. Add both half reactions.
Example1: Acid medium.
MnO4-1 + SO32- → Mn+2 + SO42-
In this reaction the oxidation number of ‘Mn’ changed from ‘+7 to +2’ that means it is reduced and ‘MnO4-1’ is an oxidising agent. The oxidation number of ‘S’ in ‘SO32-‘ changed from ‘+4 to +6’ that means it is oxidised and ‘SO32-‘ is reducing agent.
MnO4-1 → Mn+2——– is reduction half reaction.
SO32-→ SO42-———– is oxidation half reaction.
Balancing of oxidation half reaction.
SO32- → SO42-
SO32- + H2O → SO42- ———— oxygen atoms balanced.
SO32- + H2O → SO42- + 2H+1 ———— hydrogen atoms balanced.
SO32- + H2O → SO42- + 2H+1 + 2e-1 ——– charge balanced by adding electrons.
Balancing of reduction half reaction.
MnO4-1→ Mn+2
MnO4-1→ Mn+2+ 4 H2O ———— oxygen atoms balanced.
MnO4-1 + 8H+1 → Mn+2 + 4 H2O ———— hydrogen atoms balanced.
MnO4-1 + 8H+1 + 5e-1 → Mn+2 + 4 H2O ———— charge balanced by adding electrons.
To balance loss and gain electrons oxidation half reaction is multiplied by ‘5’.
To balance loss and gain electrons reduction half reaction is multiplied by ‘2’.
5SO32- + 5H2O → 5SO42- + 10H+1 + 10e-1
2 MnO4-1 + 16 H+1 + 10 e-1 → 2Mn+2 + 8 H2O
Now add the two equations by cancelling electrons and balancing ‘H2O’ and ‘H+1’ ions.
2 MnO4-1 + 6 H+1 + 5SO32- → 2Mn+2 + 5SO42- + 3 H2O
Example 2: Acid medium.
Cr2O72- + NO2-1 → Cr+3 + NO3-1
In this reaction the oxidation number of ‘Cr’ changed from ‘+6 to +3’ that means it is reduced and ‘Cr2O72’ is an oxidising agent. The oxidation number of ‘N’ in ‘NO2-1’changed from ‘+3 to +5’ that means it is oxidised and ‘NO2-1‘ is reducing agent.
Cr2O72- → Cr+3 ———- reduction half reaction.
NO2-1 → NO3-1 ———- oxidation half reaction
Balancing of oxidation half reaction.
NO2-1 → NO3-1
NO2-1 + H2O → NO3-1 —————– oxygen atoms are balanced.
NO2-1 + H2O → NO3-1 + 2H+1 ——-Hydrogen atoms are balanced.
NO2-1 + H2O → NO3-1 + 2H+1 + 2e-1 —Charge balanced by adding electrons.
Balancing of reduction half reaction.
Cr2O72-→ Cr+3
Cr2O72-→Cr+3 + 7H2O —————– oxygen atoms are balanced.
Cr2O72- + 14H+1→ Cr+3 + 7H2O ——- Hydrogen atoms are balanced.
Cr2O72- + 14H+1→ 2Cr+3 + 7H2O ——other atoms are balanced.
Cr2O72- + 14H+1 + 6e-1 → 2Cr+3 + 7H2O —— Charge balanced by adding electrons.
To balance loss and gain electrons oxidation half reaction is multiplied by ‘6’.
To balance loss and gain electrons reduction half reaction is multiplied by ‘2’.
6NO2-1 + 6H2O → 6NO3-1 + 12H+1 + 12e-1
2Cr2O72- + 28H+1 + 12e-1 → 4Cr+3 + 14H2O
Now add the two equations by cancelling electrons and balancing ‘H2O’ and ‘H+1’ ions.
2Cr2O72- + 6NO2-1 + 16H+1 → 4Cr+3 + 6NO3-1 + 8H2O
Or
Cr2O72- + 3NO2-1 + 8H+1 → 2Cr+3 + 3NO3-1 + 4H2O
Now let us see the examples in basic medium.
Example 3:
Cr(OH)3 + IO3-1 → CrO4-2 + I-1
In this reaction the oxidation number of ‘Cr’ changed from ‘+3 to +6’ that means it is oxidised and ‘Cr(OH)3’ is a reducing agent. The oxidation number of ‘I’ in ‘IO3-1’changed from
‘+5 to -1’ that means it is reduced and ‘IO3-1’ is oxidising agent.
Cr(OH)3 → CrO4-2 —————oxidation half reaction.
IO3-1 → I-1 ——————reduction half reaction.
Balancing of oxidation half reaction.
Cr(OH)3 → CrO4-2
Cr(OH)3 + H2O → CrO4-2 ———–oxygen atoms are balanced.
Cr(OH)3 + H2O + 5(OH)-1 → CrO4-2 + 5H2O ——hydrogen atoms are balanced.
Cr(OH)3 + H2O + 5(OH)-1 → CrO4-2 + 5H2O + 3e-1 —–charge balanced.
Balancing of reduction half reaction.
IO3-1 → I-1
IO3-1 → I-1 +3H2O ————oxygen atoms are balanced.
IO3-1 + 6H2O → I-1 +3H2O + 6(OH)-1 ——–hydrogen atoms are balanced.
IO3-1 + 6H2O + 6e-1 → I-1 +3H2O + 6(OH)-1 —– charge balanced.
To balance loss and gain electrons oxidation half reaction is multiplied by ‘6’.
To balance loss and gain electrons reduction half reaction is multiplied by ‘3’.
6Cr(OH)3 +6 H2O + 30(OH)-1 → 6CrO4-2 + 30H2O + 18e-1
3IO3-1 + 18H2O + 18e-1 → 3I-1 +9H2O +18(OH)-1
Now add the two equations by cancelling electrons and balancing ‘H2O’ and ‘(OH)-1 ions.
6Cr(OH)3 + 3IO3-1 + 12(OH)-1 → 6CrO4-2 + 3I-1 + 15H2O
Or
2Cr(OH)3 + IO3-1 + 4(OH)-1 → 2CrO4-2 + I-1 + 5H2O
Example 4:
Cl2 → Cl-1 + ClO-1
In this reaction in basic medium Cl2 changed to ‘Cl-1’. Oxidation number changed from 0 to -1. That is decrease in oxidation number and it is reduction. It is reduction half reaction and ‘Cl2’ is oxidising agent.
In this reaction in basic medium Cl2 changed to ‘ClO-1’. Oxidation number changed from ‘0 to +1’. That is increase in oxidation number and it is oxidation. It isoxidation half reaction and ‘Cl2’ is reducing agent.
Cl2 → ClO-1 ——–oxidation half reaction.
Cl2 → Cl-1 ———reduction half reaction.
Balancing of oxidation half reaction.
Cl2 → ClO-1
Cl2 → 2ClO-1
Cl2 + 2H2O → 2ClO-1 ——-oxygen atoms are balanced.
Cl2 + 2H2O + 4(OH)-1 → 2ClO-1 + 4H2O ——hydrogen atoms are balanced.
Cl2 + 2H2O + 4(OH)-1 → 2ClO-1 + 4H2O + 2e-1 ——charge balanced.
Balancing of reduction half reaction.
Cl2 → Cl-1
Cl2 → 2Cl-1
Cl2 + 2e-1 → 2Cl-1 —–charge balanced.
Now add the two equations.
Cl2 + 2H2O + 4(OH)-1 + Cl2 + 2e-1 → 2ClO-1 + 4H2O + 2e-1 + 2Cl-1
Now cancel charges and balance ‘H2O’ and (OH)-1 ions on both sides.
2Cl2 + 4(OH)-1 → 2ClO-1 + 2H2O + 2Cl-1
Or
Cl2+ 2(OH)-1 → ClO-1+ Cl-1 + H2O
Now we go to another concept of chemical equations where energy changes are involved.
To understand such reactions we need to understand the following concepts.
Energy, Heat, and Temperature.
When a chemical reaction occurs, there are frequently visual signals such as colour change, evolution of gases, precipitation of substances and energy changes.
Energy is powerful but abstract physical concept that describes the ability to do work.
It is of great public interest at the present time. There are methods for safe, efficient and economical conversions of one form of energy to another.
In a broader sense energy can be classified as potential and kinetic. Potential energy is that which arises from position; kinetic energy is that which arises from motion.
It is easier to grasp the concept of kinetic energy since it is simple to visualize the motion of an object, a particle, or any entity having mass. By definition, kinetic energy is equal to mv², where m is the mass of the moving object and v is its velocity or speed of motion.
Potential energy is more subtle. It comes about because there are forces between particles, and it requires work when we go from one relative arrangement of particles to another.
It changes when there is a change in position from one height to another, during vibratory motion during oscillatory motion etc.,
To have a better understanding let us take an example, when zinc reacts with sulfur to form zinc sulfide,
Zn +S → ZnS
The zinc atoms change from an environment where they are completely surrounded by other zinc atoms to one where they are surrounded by sulfur atoms.
Similarly, the sulfur atoms go from a state where they are joined to other sulfur atoms to a state where they are joined to zinc atoms.
Clearly we expect a change in the potential energy of the system in going from Zn + S to ZnS. This change in potential energy, which may be up or down, usually shows up as heat, but may also appear as light, sound, shock waves, or any other of the numerous manifestations of energy. Most commonly, the energy change appears as heat, either evolved to the surroundings, in which case the chemical change is said to be exothermic, or absorbed from the surroundings, in which case the chemical change is said to be endothermic.
How does one tell the difference? If the change is exothermic, the reaction mixture generally gets warmer; if endothermic, it gets colder.
There may be a complication, however, in that some reagents do not react when they are just mixed together. Often the reaction mixture must be heated to get the reaction started.
As an example, when powdered zinc is mixed with powdered sulfur, nothing happens. The mixture has to be heated, at which point it takes off and gets quite a bit hotter without input of more heat. The heat that is required to get a reaction going has nothing to do with whether the reaction is exothermic or endothermic. What counts is whether there is net evolution or absorption of heat when reactants convert to products. The net heat liberated or absorbed, when referred to standard quantities (moles) of material, is called the heat of the reaction.
Temperature is often confused with heat, but the terms are not synonymous. Heat is a quantity of energy, whereas temperature describes the intensity of heat.
The distinction may be made clear by noting that a burning match stick and a bonfire (large open air fire) can be at the same temperature, but there is more heat in bonfire.
A given quantity of heat will raise the temperature of a teaspoon of water more than it will raise the temperature of a bucket of water.
Temperature is a property that fixes the direction of heat flow. Heat always flows from body at high temperature to a body at low temperature.
ENTHALPY AND HEAT CAPACITY
In talking about the energy of a system, we tend to focus our attention on internal forms of energy such as vibration motion of atoms, kinetic energy of molecules, and potential energy stored in chemical bonds. However, there is another, more subtle contribution to the energy. It comes from the fact that the system has a volume V and is generally under the pressure of the surrounding atmosphere P. External work of the amount PV had to be done against the surrounding atmosphere to make room for the system. So, any system that has a finite volume V and is subject to a finite pressure P has energy associated with it of amount PV. Any changes in PV have to be accounted for in counting up the total energy. For this purpose, we introduce a new concept called the enthalpy, designated by H, which is the sum of the internal energy E and the external work PV. Thus, we can write, per mole of substance,
H (Enthalpy) = E (Internal energy) + PV (External work)
An increase in enthalpy 𝝙H is made up of two parts:
(1) Increase in energy 𝝙E and (2) increase in the PV product 𝝙PV.
Symbolically, this is expressed as follows
𝝙H=𝝙E+𝝙(PV)
The change in the PV product can come about because of a change in P, a change in V, or both. We shall generally restrict ourselves to situations where P is constant. In such cases, (PV) is just P𝝙V, the work done on constant- pressure surroundings by a volume change 𝝙V. Thus, at constant pressure
𝝙H = 𝝙E + P𝝙V
Or
𝝙E =𝝙H – P𝝙V
Comparison of this last relation with the first law 𝝙E=(q-w) shows that if the only work ‘w’ done by the system is P𝝙V work, then at constant pressure 𝝙H=q In other words, the enthalpy increase 𝝙H is equal to the heat absorbed by the system at constant pressure. (For this reason H is sometimes referred to as the heat content of the system, although the term “enthalpy” is preferred.) If heat is added to a system at constant pressure, part of the heat is used to increase the internal energy of the system, and the rest is used to do work on the surroundings.
*Note that the product PV is an energy measure. Putting P in atmospheres and V in liters we have liter atmospheres, as in the gas constant R (0.08206 liter atm mol-1 deg -1). One liter atmosphere equals 101.32 joules.
Exothermic and Endothermic Reactions:
Certain chemical reactions are accompanied by evolution of heat while others are accompanied by absorption of heat. The reaction which takes place with the evolution of heat is called an exothermic reaction; one in which heat is absorbed is called endothermic reaction.
The direction of heat change in a chemical reaction is often indicated qualitatively by including the word “heat” in the equation.
2Mg(s) + O2 (g) → 2MgO(s) + heat. It is an exothermic reaction.
2HgO(s) + heat → 2Hg(1)+O2(g). It is an endothermic reaction.
It may be kept in mind that the heat change expression in this way, always refers to the overall effect of the reaction.
Thermochemical Equations:
We are often interested not only in the direction of the heat change in a reaction but also in the amount of heat absorbed or evolved.
Thermo chemical equation is one in which the heat change is numerically expressed.
The heat change in such equations is always expressed in terms of moles of reactants and products.
C(s)+O2(g) → CO₂(g) + 94.4 kcal. This is the amount of heat evolved when one mole of CO2 is formed.
2HgO(s) + 43.4 kcal → 2Hg(s) + O2(g)
Thus 43.4 kcal in this equation is the amount of heat absorbed when two moles of mercuric oxide decompose to form two moles of mercury and one mole of oxygen.
A chemical equation is said to be thermally balanced, if besides fulfilling other conditions of an equation, it expresses quantity of the heat absorbed or evolved in a reaction.
